تعریف.معادله مشخصه یک عملگر خطی f معادله فرم است ، جایی که λ هر عدد واقعی است ، A ماتریس عملگر خطی است ، E ماتریس واحد از همان ترتیب است.
چند جمله ای تماس گرفت چند جمله ای مشخصهماتریس A (عملگر خطی f). در شکل ماتریسی ، معادله مشخصه به شرح زیر است:
 یا
یا
 .
.
بنابراین ، با برابر کردن چند جمله ای مشخصه با صفر ، معادله درجه را بدست می آوریم n، جایی که λ ناشناخته است ، مقادیر ریشه های آن را بدست می آوریم - اعداد مشخصه ماتریس داده شده. ریشه های مشخصه نقش زیادی در بسیاری از زمینه های ریاضیات ایفا می کنند. یکی از کاربردهای ریشه های مشخص را در نظر بگیرید - یک ابزار بسیار مهم در مطالعه فضاهای خطی و همچنین در حل بسیاری از مسائل کاربردی جبر خطی.
مجموعه همه ریشه های معادله مشخصه را طیف عملگر می نامند f(هر ریشه با تعدد موجود در معادله مشخصه در نظر گرفته می شود).
مثال.ریشه های مشخصه ماتریس را بیابید.
بیایید ماتریس را بسازیم

با برابر کردن چند جمله ای مشخصه با صفر ، معادله درجه دوم را بدست می آوریم
سپس ریشه های معادله هستند ![]() .
.
تعریف.بگذارید f یک عملگر خطی فضا باشد و بردار غیر صفر باشد که برابر آن است
یک عدد واقعی کجاست سپس بردار را بردار ویژه عملگر و ماتریس تعریف کننده آن می نامیم ، - ارزش ویژه ، یا ارزش ویژه تبدیل. گفته می شود که بردار ویژه به ارزش ویژه اشاره دارد.
بردارهای ویژه نقش مهمی را هم در خود ریاضیات و هم در کاربردهای آن ایفا می کنند. به عنوان مثال ، رزونانس ، که در آن فرکانس های طبیعی نوسانات سیستم با فرکانس نوسانات نیروهای خارجی منطبق است. در ریاضیات ، بردارهای ویژه در حل سیستمهای معادلات دیفرانسیل مفید هستند.
قضیه اگر عملگر خطی f در مبنا (مبنای اول) دارای ماتریس A و در مبنا (مبنای دوم) - ماتریس B باشد ، پس برابری صادق است:
در نتیجه ، هنگام عبور از مبنای جدید ، چند جمله ای مشخصه عملگر خطی تغییر نمی کند.
T اگر T ماتریس انتقال از مبنای اول به دوم باشد ، پس. سپس ما سمت راست برابری را تغییر می دهیم ●
قضیه... برای این که عدد λ 0 از میدان P دارای ارزش ویژه بردار فضای L n روی P باشد ، لازم و کافی است که عدد λ 0 ریشه مشخصه عملگر f باشد.
سند من.نیاز. بگذار باشد λ 0 ارزش ویژه اپراتور f، سپس در لوگاریتمبردار ویژه ای وجود دارد که
بگذار باشد ![]() آیا خط مختصات آن در برخی از اساس ، پس
آیا خط مختصات آن در برخی از اساس ، پس
از سوی دیگر ، از آن زمان که ، ماتریس عملگر خطی در یک مبنای مشخص کجاست ، پس
با برابر کردن سمت راست (1) و (2) ، بدست می آوریم:
 (3)
(3)
معادلات (3) به معنای بردار عددی با مختصات است ![]() یک راه حل برای سیستم معادلات زیر است (4).
یک راه حل برای سیستم معادلات زیر است (4).
 (4)
(4)
بردار با صفر متفاوت است (زیرا مناسب است) ، بنابراین سیستم (4) دارای راه حل غیر صفر است ، بنابراین تعیین کننده آن 0 است.
 (5)
(5)
و از این رو تعیین کننده منتقل شده برابر 0 است.
![]() (6)
(6)
بدین ترتیب، λ 0 ریشه معادله مشخصه است.
IIکفایت بگذار باشد λ 0
ریشه مشخصه اپراتور در برخی موارد است ![]() ... اجازه دهید آن را ثابت کنیم λ 0
مقدار ویژه عملگر A است.
... اجازه دهید آن را ثابت کنیم λ 0
مقدار ویژه عملگر A است.
در واقع ، اگر λ 0 آیا ریشه مشخصه است ، بنابراین برابری (6) ، و در نتیجه برابری (5) ، و این بدان معناست که سیستم (4) دارای راه حل های غیر صفر است.
اجازه دهید راه حل غیر صفر سیستم (4) را انتخاب کنیم: بردار عددی ![]() ... سپس مساوی (3) برقرار است.
... سپس مساوی (3) برقرار است.
بردار را در نظر بگیرید ، و برای آن برابری (2) برقرار است و بر اساس فرمول ، برابری (1) صادق است ، ماتریس عملگر در کجا قرار دارد V... این برابری را نشان می دهد ، به این معنی که بردار یک بردار ویژه عملگر است ، که با مقدار ویژه مطابقت دارد λ 0 ... این چیزی بود که باید اثبات می شد. قضیه اثبات شده است.
اظهار نظر.به منظور یافتن مقادیر ویژه عملگر ، لازم است معادله ای ساخته و حل شود (5). برای یافتن بردارهای ویژه اپراتور ، لازم است سیستم معادلات (4) را تهیه کرده و مجموعه اساسی راه حل های این سیستم را بیابید.
برای کنترل صحت محاسبه مقادیر ویژه (آنها می توانند تصادفی ، پیچیده باشند) ، از دو واقعیت استفاده می شود:
1)  ، جایی که آخرین جمع اثری از ماتریس مجموع عناصر مورب است.
، جایی که آخرین جمع اثری از ماتریس مجموع عناصر مورب است.
2)  .
.
مثال.مقادیر ویژه و بردارهای ویژه را بیابید  .
.
 برابر با صفر می گیریم. ...
برابر با صفر می گیریم. ...
3) . , ![]() .
.

اجازه دهید یک متغیر رایگان باشد ، سپس یک بردار دریافت می کنیم  .
.
تمرین. برای بردار بررسی کنید.
 .
.
معادله مشخصه عبارت است از:
برای تعیین نوع جزء آزاد ، لازم است که معادله مشخصه را بسازید و حل کنید: z (p) = 0 برای نوشتن معادله مشخصه ، لازم است یک نمودار رسم کنید که در آن همه منابع EMF و جریان باید جایگزین شوند مقاومت داخلی خود را دارند ، و مقاومت سلفی و خازنی باید به ترتیب برابر Pl باشد و بعلاوه ، لازم است که هر شاخه ای از این مدار شکسته شود ، مقاومت اولیه آن نسبت به نقاط شکست نوشته شود ، آن را به صفر برسانیم ، حل کنیم و ریشه های p را تعیین کنید ، اگر ریشه ها منفی واقعی بودند ، سپس جزء آزاد تابع مورد نظر:
 ، جایی که m تعداد ریشه های معادله است ؛
، جایی که m تعداد ریشه های معادله است ؛
ریشه ها ؛ قابل ادغام دائمی
اگر ریشه های معادله کاراکتر ترکیبی پیچیده باشد ، حالت آزاد شکل زیر را خواهد داشت:
 فرکانس ارتعاشات آزاد کجاست.
فرکانس ارتعاشات آزاد کجاست.
مرحله اولیه ارتعاشات آزاد.
8. زمان گذرا. تعیین عملاً t pp. محاسبه زمان گذرا.
زمان فرایند گذرا به ضریب میرایی بستگی دارد. مقدار معکوس ثابت زمان نامیده می شود و نشان دهنده زمانی است که طی آن مقدار جزء آزاد فرآیند گذرا با ضریب e = 2.72 کاهش می یابد. مقدار بستگی به مدار و پارامترها دارد. برای مدار با اتصال سری r و L = ، و برای اتصال سری
95٪ پایان گذرا 3.
ساختن منحنی های اجزای آزاد فرایند گذرا با تنظیم زمان t مقادیر 0 ، 2 ... آسان تر است. شرایط (شکل 1.)
تصویر 1:

9.10 ، فرآیند گذرا در r ، C - مدار هنگام روشن شدن به منبع ولتاژ ثابت. انجام تجزیه و تحلیل با روش کلاسیک ؛ عبارات تحلیلی برای U C (t) ارائه دهید ؛ فناوری اطلاعات و ارتباطات)؛ گرافیک (روش کلاسیک).
معادله حالت مدار rC پس از تغییر به شرح زیر است:
![]() (1) ، یا rC (2)
(1) ، یا rC (2)
راه حل او: ![]()
خازن C ، پس از بسته شدن کلید در t ، به مقدار حالت پایدار شارژ می شود.
از آنجا که شرایط اولیه صفر است ، طبق قانون جابجایی ![]() برای t = 0 ، یا 0 = A ، از آنجا A = -E.
برای t = 0 ، یا 0 = A ، از آنجا A = -E.
راه حل معادله (2) به شکل زیر خواهد بود:
جریان مدار i (t) = C
تصویر 1

شکل 2.

نمودارهای تغییرات ولتاژ و جریان i (t) در شکل های 1 و 2 نشان داده شده است. از نمودارها می توان دریافت که ولتاژ خازن به صورت نمایی از 0 به E افزایش می یابد ، در حالی که جریان در لحظه تغییر ناگهانی به مقدار E / r ، و سپس کاهش می یابد تا خراشیده شود.
11.12 فرآیند گذرا در مدار r ، C - هنگام اتصال به منبع ولتاژ سینوسی. انجام تجزیه و تحلیل با روش کلاسیک ؛ عبارات تحلیلی برای U C (t) ارائه دهید ؛ فناوری اطلاعات و ارتباطات)؛ گرافیک (روش کلاسیک).

معادله حالت مدار rC در حالت گذرا به شرح زیر است
rC ![]() .
.
راه حل این معادله:
![]()
جزء رایگان
![]() جایی = rC
جایی = rC
از آنجا که مدار خطی است ، پس با یک اثر سینوسی و در یک حالت ثابت ، ولتاژ خازن نیز بر اساس یک قانون سینوسی با فرکانس عمل ورودی تغییر می کند ، بنابراین ، برای تعیین = ، ما از روش دامنه های پیچیده:
![]() ;
; 
![]()
با در نظر گرفتن اینکه j = ، بدست می آوریم:
ثابت ادغام A جزء آزاد
اجازه دهید از شرایط اولیه در مدار ، با در نظر گرفتن قانون جابجایی استفاده کنیم:
![]() برای t = 0 ، آخرین عبارت دارای فرم است
برای t = 0 ، آخرین عبارت دارای فرم است
از کجا A = -
با افزودن اجزاء و بیان نهایی ولتاژ خازن در حالت گذرا را بدست می آوریم:
= + = ![]() - (1)
- (1)
تجزیه و تحلیل بیان (1) نشان می دهد که فرآیند گذرا در مدار rC تحت عمل سینوسی بستگی به فاز اولیه EMF منبع در لحظه سوئیچینگ و ثابت زمان مدار rC دارد.
اگر ، سپس = 0 و در مدار بلافاصله پس از تغییر حالت ثابت ایجاد می شود ، یعنی
در ولتاژ = -، یعنی ولتاژ خازن بلافاصله پس از تغییر می تواند تقریباً دو برابر علامت مثبت شود و سپس به تدریج به = نزدیک می شود.
تفاوت فاز معادله (1) را به شکل زیر می آورد:
تفاوت بین این حالت و حالت قبلی این است که ولتاژ خازن بلافاصله پس از تغییر می تواند تقریباً دو برابر علامت منفی برسد.
برای مدار Rc در نظر گرفته شده با منبع جریان سینوسی در حالت حالت پایدار ، فاز اولیه ولتاژ ورودی هیچ نقشی ایفا نمی کند ، اما تأثیر آن در فرایند گذرا قابل توجه است.
13. فرآیند گذرا در مدارات r ، L ، C - هنگام اتصال به منبع ولتاژ ثابت. فرایند دوره ای. عبارات تحلیلی برای i (t) ، نمودارها. (روش کلاسیک).
ریشه ها واقعی ، منفی ، متفاوت هستند.
I (t) = + A1e p 1 t + A2e p 2 t را تنظیم کردم
روند به صورت دوره ای است:
t = 0 (i (0) = A1 + A2 ؛ A1 = -A2
{ ![]()
t = 0 i l (0) * r + L + Uc (0) = E A1 = -A2 = ()
i l (t) = ( ![]() )
)
14. فرآیند گذرا در مدارات r ، L ، C - هنگام اتصال به منبع ولتاژ ثابت. فرآیند بحرانی عبارات تحلیلی برای i (t) ، نمودارها. (روش کلاسیک).
i l (t) = i + (B1 + B2 * t) *
t = 0: i l (0) = β1 = 0
![]()
اگر ریشه ها واقعی ، منفی ، مساوی باشد ، این فرایند بسیار مهم است.

15. فرآیند گذرا در مدارات r ، L ، C - هنگام اتصال به منبع ولتاژ ثابت. فرایند نوسانی. بیان تحلیلی برای i (t) ، نمودارها. (روش کلاسیک).
P t = -δ ± j * ω sv ω sv =
ریشه های منفی منفی ، تا حدی مزدوج پیچیده.
i l (t) = i A1e - δt * sin (ω sv t + ψ)

i l (t) = i دهان + (M * cos ω sv t + N * sin ω sv t) *
i l (t) = * ![]() = *
= *

16. فرآیند گذرا در مدار r ، L ، C - هنگام اتصال به منبع ولتاژ سینوسی. فرایند دوره ای بیان تحلیلی برای i (t) ، نمودارها. (روش کلاسیک).
R (t) = E max * sin (ωt + ψ)
2. 
در حالت کلاسیک ، تعداد معادلات در این حالت برابر با تعداد شاخه های مدار است
روش ، راه حل در قالب مجموع راه حل های عمومی و خاص یافت می شود. محاسبه فرآیند گذرا با سیستم معادلات دیفرانسیل معمولی که توسط یکی از روشهای محاسبه برای مقادیر لحظه ای توابع زمان گردآوری شده است ، توصیف می شود. راه حل هر متغیر این سیستم به عنوان مجموع راه حل های عمومی و خاص یافت می شود. برای تدوین معادله می توان از موارد زیر استفاده کرد: روشی مبتنی بر اعمال قوانین Kirchhoff ، روش پتانسیل های گره ، روش جریان حلقه و غیره. به عنوان مثال ، یک سیستم معادلات دیفرانسیل ، که پس از تغییر طبق قوانین اول و دوم Kirchhoff تدوین شده است ، شکل زیر را دارد:
مثلا،
تعداد معادلات در این مورد برابر با تعداد شاخه های مدار است. بگذارید لازم باشد که i k فعلی را در شاخه با شماره K. بیابیم بدون اینکه جریانهای شاخه ها پی در پی باشد ، در نتیجه ما i k فعلی و مشتقات آن را به ترتیب n بدست می آوریم:

ترتیب معادله دیفرانسیل n با تعداد عناصر مدار واکنش پذیر مستقل (m) تعیین می شود. معمولاً n = m ، اما بسته به روش اتصال ، ممکن است به گونه ای باشد که n عناصر خازنی متصل به سری را می توان با یک عنصر جایگزین کرد ، همانطور که عناصر استقرایی متصل به موازات را می توان با یک معادل جایگزین کرد. شکل 9.5 جایگزینی 2 مخزن سری با یک معادل را نشان می دهد. در حالت کلی ، ترتیب معادله دیفرانسیل n است: n = n lc -n ce -n lj ، جایی که n lc تعداد عناصر واکنشی (L و C) در مدار است ، n ce تعداد خازنی است مدارها ، n lj تعداد گره ها یا مقاطع استقرایی است. خازنی به معنی مدار متشکل از عناصر خازنی یا عناصر خازنی و منابع ایده آل EMF است ، شکل 9.6.a. القایی به معنی گره ای است که شاخه های القایی یا شاخه های استقرایی و منابع جاری در آن همگرا می شوند (شکل 9.6.ب) ، یا بخش هایی که فقط عبور از شاخه های استقرایی یا شاخه های استقرایی و منابع جاری. توجه داشته باشید که مرحله ترسیم معادله دیفرانسیل اجباری نیست و بدون ترسیم معادله می توان جریان یا ولتاژ گذرا را یافت. همانطور که نشان داده شد ، در روش کلاسیک برای محاسبه فرآیندهای گذرا ، معادلات را حل می کنیم یک راه حل خاص رژیمی به نام اجباری را توصیف می کند. راه حل معادله همگن (سمت راست مساوی با صفر) در غیاب EMF خارجی و منابع فعلی فرآیند را توصیف می کند و آزاد نامیده می شود. بر این اساس ، جریانهای آزاد و اجباری ، ولتاژها ، بارها در نظر گرفته می شوند. بنابراین ، جریان در شاخه با عدد K به عنوان یک مجموع نشان داده می شود. ) آ = ||یک ik||n 1 با تفریق λ از عناصر مورب. این تعیین کننده نسبت به X - چند جمله ای مشخصه ، چند جمله ای است. در شکل باز شده H. y چنین نوشته شده است: جایی که S 1 = یک 11 + یک 22 +...
یک nn- به اصطلاح ردیابی ماتریس ، S 2- مجموع همه خردسالان اصلی مرتبه 2 ، یعنی خردسالان فرم i k) ، و غیره ، و S n- تعیین کننده ماتریس آ... Roots H. y λ 1، λ 2، ...، λ nمقادیر ویژه ماتریس نامیده می شوند آ... برای یک ماتریس متقارن واقعی ، و همچنین برای ماتریس هرمیتی ، همه λ کواقعی هستند ، برای یک ماتریس کج متقارن واقعی همه λ کاعداد کاملاً خیالی ؛ در مورد یک ماتریس متعامد واقعی ، و همچنین یک ماتریس واحد ، همه | λ ک| = 1. H. y در زمینه های مختلف ریاضیات ، مکانیک ، فیزیک ، فناوری یافت می شوند. در نجوم ، هنگام تعیین اغتشاشات سکولار سیارات ، آنها نیز به H. y می رسند. از این رو نام دوم H. y است. - معادله سکولار 2) H. y معادله دیفرانسیل خطی با ضرایب ثابت یک 0λ y (n) + یک سال (n-1) +... + a n-1 y " + a n y = 0 یک معادله جبری که پس از جایگزینی تابع از یک معادله دیفرانسیل معین بدست می آید درو مشتقات آن توسط قدرتهای مربوطه λ ، یعنی معادله یک 0λ n + یک 1λ n-1 +
... +
a n-1 y " + a n y = 0. این معادله هنگام جستجوی راه حل خاصی از فرم به دست می آید در = ببین λ NSبرای یک معادله دیفرانسیل داده شده برای سیستم معادلات دیفرانسیل خطی H. y با استفاده از واجد شرایط نوشته شده است H. y ماتریس ها آ = دائرclالمعارف بزرگ شوروی. - م .: دائرclالمعارف شوروی.
1969-1978
.
در بسیاری از موارد ، فرایندهای فیزیکی رخ داده در سیستم ها توسط سیستمی از معادلات دیفرانسیل خطی معمولی با ضرایب ثابت توصیف می شود ، که در یک حالت نسبتاً کلی می توان آن را به یک معادله دیفرانسیل تقلیل داد ... دایره المعارف فناوری معادله جبری فرم تعیین کننده در این فرمول از تفریق مقدار x از عناصر مورب بدست می آید. این یک چند جمله ای در x است و چند جمله ای مشخص نامیده می شود ... فرهنگ لغت دائرclالمعارف معادله مشخصه- - [V.A. Semenov. انگلیسی روسی فرهنگ لغت حفاظت] مباحث رله حفاظت EN معادله مشخصه ... راهنمای مترجم فنی معادله جبری شکل. تعیین کننده در این فرمول از تعیین کننده ماتریس x از عناصر مورب بدست می آید. این یک چند جمله ای در x است و چند جمله ای مشخص نامیده می شود. * * * مشخصه ... ... فرهنگ لغت دائرclالمعارف معادله مشخصه- būdingoji lygtis statusas T sritis automatika atitikmenys: angl. معادله مشخصه ؛ معادله عملکرد vok. charakteristische Gleichung، f؛ Stammgleichung ، f rus. معادله مشخصه ، n pranc. équation caractéristique، f… Automatikos terminų žodynas معادله مشخصه- būdingoji lygtis statusas T sritis fizika atitikmenys: angl. معادله مشخصه ؛ معادله عملکرد vok. charakteristische Gleichung ، f rus. معادله مشخصه ، n pranc. équation caractéristique، f ... Fizikos terminų žodynas معادله مشخصه دانشنامه "هوانوردی" معادله مشخصه- معادله مشخصه در بسیاری از موارد ، فرایندهای فیزیکی رخ داده در سیستم ها توسط سیستمی از معادلات دیفرانسیل خطی معمولی با ضرایب ثابت توصیف می شود که در حالت نسبتاً کلی می توان آنها را کاهش داد ... دانشنامه "هوانوردی" معادله قدیمی ، هنر را ببینید. چند جمله ای مشخصه ... دانشنامه ریاضیات چند جمله ای مشخص چند جمله ای است که مقادیر ویژه یک ماتریس را تعیین می کند. معنای دیگر: چند جمله ای مشخص یک تکرار خطی چند جمله ای است. مطالب 1 تعریف ... ویکی پدیا معادله مشخصه پس از تعویض برای مدار ترسیم می شود. می توان آن را به روش های زیر بدست آورد: طبق اولین روش در سخنرانی قبلی ، یک معادله دیفرانسیل برای ولتاژ یک خازن برای یک مدار سریال R-L-C بدست آمد که بر اساس آن یک معادله مشخصه نوشته شده است. لازم به ذکر است ، از آنجا که مدار خطی تحت یک فرآیند گذرا قرار می گیرد ، ریشه های معادله مشخصه برای همه اجزای آزاد ولتاژها و جریانهای شاخه های مدار مشترک است ، پارامترهای آن در معادله مشخصه گنجانده شده است. به بنابراین ، با توجه به اولین روش ترسیم معادله مشخصه ، می توان هر متغیری را که نسبت به آن نوشته شده است ، انتخاب کرد. اجازه دهید کاربرد روشهای دوم و سوم رسم معادله مشخصه با استفاده از مثال مدار در شکل را در نظر بگیریم. 1 ترسیم معادله مشخصه با استفاده از روش امپدانس ورودی به شرح زیر است: مقاومت ورودی مدار AC ثبت می شود. jw توسط عملگر p جایگزین می شود. عبارت به دست آمده صفر است. معادله با ویژگی مطابقت دارد باید تاکید کرد که امپدانس ورودی را می توان نسبت به نقطه شکست هر شاخه ای از مدار نوشت. در این حالت ، شبکه فعال دو ترمینال به صورت شباهت با روش ژنراتور معادل با یک شبکه منفعل جایگزین می شود. این روش برای ترسیم معادله مشخصه ، عدم وجود شاخه های مغناطیسی در مدار را فرض می کند. در صورت وجود ، لازم است عملیات بازکردن اولیه آنها انجام شود. برای مدار در شکل. 1 با توجه به پایانه های منبع با جایگزینی jw با p و برابر شدن عبارت حاصله با صفر ، می نویسیم هنگام تنظیم معادله مشخصه بر اساس بیان عامل اصلی ، تعداد معادلات جبری که بر اساس آنها نوشته شده است برابر با تعداد اجزای آزاد ناشناخته جریان است. جبر سیستم اصلی معادلات انتگرال دیفرانسیل ، که به عنوان مثال ، بر اساس قوانین Kirchhoff یا با روش جریان حلقه ، تدوین شده است ، با جایگزینی نمادهای تمایز و ادغام ، به ترتیب با ضرب و تقسیم توسط اپراتور ص. معادله مشخصه با برابر کردن تعیین کننده ثبت شده به صفر بدست می آید. از آنجا که عبارت تعیین کننده اصلی به طرف راست سیستم معادلات ناهمگن بستگی ندارد ، می توان آن را بر اساس یک سیستم معادلات که برای کل جریانها نوشته شده است ، ترسیم کرد. برای مدار در شکل. 1 سیستم جبری معادلات بر اساس روش حلقه جریان دارد بنابراین عبارت اصلی تعیین کننده اصلی این سیستم است معادل D به صفر ، نتیجه ای مشابه (1) بدست می آوریم. روش کلی برای محاسبه فرآیندهای گذرا با روش کلاسیک به طور کلی ، روش محاسبه فرآیندهای گذرا با روش کلاسیک شامل مراحل زیر است: نمونه هایی از محاسبه فرآیندهای گذرا با استفاده از روش کلاسیک 1. فرآیندهای گذرا در مدار R-L هنگامی که به منبع ولتاژ متصل می شود چنین فرایندهایی اتفاق می افتد ، به عنوان مثال ، هنگامی که الکترومغناطیس ، ترانسفورماتور ، موتورهای الکتریکی و غیره به منبع تغذیه متصل می شوند. دو مورد را در نظر بگیرید: با توجه به روش در نظر گرفته شده برای جریان در مدار در شکل. 2 قابل نوشتن است معادله مشخصه از آنجا ثابت زمان بدین ترتیب، با جایگزینی (4) و (5) در رابطه (3) ، می نویسیم طبق اولین قانون تعویض. سپس بنابراین ، جریان در مدار در فرایند گذرا با معادله توصیف می شود و ولتاژ سلف - توسط عبارت شکل کیفی منحنی ها و مربوط به محلول های بدست آمده در شکل نشان داده شده است. 3 برای منبع نوع دوم ، جزء اجباری با استفاده از روش نمادین محاسبه می شود: بیان جزء آزاد بستگی به نوع منبع ولتاژ ندارد. از این رو ، از آن به بعد بنابراین ، ما در نهایت دریافت می کنیم تجزیه و تحلیل عبارت بدست آمده (6) نشان می دهد: اگر از نظر اندازه قابل توجه باشد ، برای نیم دوره جزء آزاد به طور قابل توجهی کاهش نمی یابد. در این حالت ، حداکثر مقدار جریان گذرا می تواند به طور قابل توجهی از دامنه جریان حالت پایدار فراتر رود. همانطور که در شکل دیده میشود. 4 کجا بنابراین ، برای یک مدار خطی ، حداکثر مقدار جریان گذرا نمی تواند از دامنه دو برابر جریان اجباری فراتر رود: به طور مشابه برای یک مدار خطی با خازن: اگر در لحظه تغییر ولتاژ اجباری برابر مقدار دامنه آن باشد و ثابت زمان مدار به اندازه کافی بزرگ باشد ، پس از حدود نیمی از دوره ولتاژ روی خازن به حداکثر مقدار خود می رسد ، که نمی تواند از دامنه دو برابر ولتاژ اجباری فراتر رود: 2. موقعی که سلف از منبع تغذیه قطع می شود هنگامی که کلید در مدار باز می شود در شکل. 5 جزء اجباری جریان از طریق سلف. معادله مشخصه جایی که طبق اولین قانون تعویض بنابراین ، عبارت جریان گذرا و ولتاژ در سلف تجزیه و تحلیل (7) نشان می دهد که وقتی مدارهای حاوی عناصر القایی باز می شوند ، ممکن است ولتاژهای زیادی ایجاد شود که بدون انجام اقدامات خاص ، می تواند به تجهیزات آسیب برساند. در واقع ، برای 3. شارژ و تخلیه خازن هنگامی که کلید به موقعیت 1 منتقل می شود (شکل 6 را ببینید) ، روند شارژ خازن شروع می شود: جزء اجباری ولتاژ در خازن. از معادله مشخصه ریشه مشخص می شود حالت آزاد مدار به منابع انرژی بستگی ندارد ، فقط با ساختار مدار و پارامترهای عناصر آن تعیین می شود. از اینجا نتیجه می گیرد که ریشه معادله مشخصه p1 ، p2 ،… ، pn برای همه توابع متغیر (جریان و ولتاژ) یکسان خواهد بود. معادله مشخصه را می توان با استفاده از روش های مختلف ساخت. اولین روش کلاسیک است ، هنگامی که معادله مشخصه کاملاً مطابق با دیفرانسیل مطابق طرح کلاسیک ترسیم می شود. هنگام محاسبه گذرا در یک مدار پیچیده ، یک سیستم معادلات دیفرانسیل "m" مطابق قوانین Kirchhoff برای نمودار مدار پس از تغییر تنظیم می شود. از آنجا که ریشه معادله مشخصه برای همه متغیرها مشترک است ، راه حل سیستم معادلات دیفرانسیل با توجه به هر متغیری (با انتخاب) انجام می شود. در نتیجه راه حل ، معادله دیفرانسیل ناهمگن با یک متغیر بدست می آید. معادله مشخصه مطابق با دیفرانسیل بدست آمده جمع آوری شده و ریشه های آن تعیین می شود. مثال. معادله مشخصه را ترسیم کرده و ریشه های آن را برای متغیرهای مدار مشخص کنید. 59.1 پارامترهای عناصر به صورت کلی تنظیم می شوند. سیستم معادلات دیفرانسیل مطابق قوانین Kirchhoff: اجازه دهید سیستم معادلات را با توجه به متغیر i3 حل کنیم ، در نتیجه معادله دیفرانسیل ناهمگن بدست می آید: راه دوم برای ایجاد معادله مشخصه این است که تعیین کننده اصلی سیستم معادلات Kirchhoff برای اجزای آزاد متغیرها را به صفر برسانید. اجازه دهید جزء رایگان یک جریان دلخواه فرم icv = Аkept داشته باشد ، سپس: سیستم معادلات اجزای آزاد از سیستم معادلات دیفرانسیل Kirchhoff با جایگزینی مشتقات متغیرها توسط عامل p و انتگرالها توسط 1 / p بدست می آید. برای مثال مورد بررسی ، سیستم معادلات اجزای آزاد به شکل زیر است: معادله مشخصه و ریشه آن: سومین روش ترسیم معادله مشخصه (مهندسی) این است که مقاومت اپراتور ورودی مدار را نسبت به هر یک از شاخه های آن برابر صفر کنیم. بنابراین مقاومت اپراتور یک عنصر از مقاومت پیچیده آن بدست می آید ، بنابراین فاکتور jω را با p جایگزین می کنیم برای مثال مورد نظر: روش سوم ساده ترین و مقرون به صرفه ترین است ، بنابراین بیشتر در محاسبه گذرا در مدارهای الکتریکی استفاده می شود. ریشه های معادله مشخصه ، یک فرآیند گذرا آزاد در یک مدار بدون منابع انرژی را مشخص می کند. چنین فرایندی با اتلاف انرژی پیش می رود و بنابراین به موقع از بین می رود. از اینجا نتیجه می گیرد که ریشه های معادله مشخصه باید منفی یا دارای یک قسمت واقعی منفی باشند. در حالت کلی ، ترتیب معادله دیفرانسیل ، که فرآیند گذرا را در مدار توصیف می کند ، و بنابراین ، درجه معادله مشخصه و تعداد ریشه های آن برابر با تعداد شرایط اولیه مستقل یا عدد است واحدهای ذخیره انرژی مستقل (سیم پیچ L و خازن C). اگر نمودار مدار شامل خازن های متصل موازی C1 ، C2 ، ... یا سیم پیچ های متصل به سری L1 ، L2 ، ... باشد ، هنگام محاسبه فرآیندهای گذرا باید آنها را با یک عنصر معادل SE = C1 + C2 + جایگزین کرد ... یا LE = L1 + L2 + ... بنابراین ، نمای کلی راه حل برای هر متغیر در محاسبه فرآیند گذرا را می توان تنها از تجزیه و تحلیل نمودار مدار ، بدون ترسیم و حل یک سیستم معادلات دیفرانسیل ، گردآوری کرد. برای مثال بالا.


 در قالب مجموع تصمیمات عمومی و خصوصی ارائه می شود.
در قالب مجموع تصمیمات عمومی و خصوصی ارائه می شود.![]()

ببینید "معادله مشخصه" در فرهنگ لغت های دیگر چیست:
کتابها

 .
.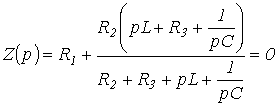
.
(1)

![]()

![]() .
. .
(5)
 .
.![]() ,
, ,
,
 .
. ,
,![]() .
. .
(6)

![]() ، حداکثر جریان در حدود اتفاق می افتد. در محدوده در
، حداکثر جریان در حدود اتفاق می افتد. در محدوده در![]() .
.
![]() ,
,![]() و
و ![]() .
. .
.
 .
.
(7)
![]() مدول ولتاژ در سلف در لحظه تغییر چند برابر بیشتر از ولتاژ منبع خواهد بود:. در غیاب مقاومت میرایی R ، ولتاژ مشخص شده روی مخاطبین باز کلید اعمال می شود ، در نتیجه یک قوس بین آنها ایجاد می شود.
مدول ولتاژ در سلف در لحظه تغییر چند برابر بیشتر از ولتاژ منبع خواهد بود:. در غیاب مقاومت میرایی R ، ولتاژ مشخص شده روی مخاطبین باز کلید اعمال می شود ، در نتیجه یک قوس بین آنها ایجاد می شود.
![]() .
.![]() ... از این رو زمان ثابت است.
... از این رو زمان ثابت است.












