Campo de fuerza. ¿Qué significa "campo de fuerza"? ¿Qué es un campo de fuerza?

Campo fisico - una forma especial de materia que une partículas de materia y transfiere (con una velocidad finita) el efecto de unos cuerpos sobre otros. Cada tipo de interacción en la naturaleza tiene su propio campo. Campo de fuerza Se denomina región del espacio en la que un cuerpo material colocado allí es actuado por una fuerza que depende (en el caso general) de las coordenadas y del tiempo. El campo de fuerza se llama estacionario, si las fuerzas que actúan en él no dependen del tiempo. Un campo de fuerza, en cualquier punto del cual la fuerza que actúa sobre un punto material dado tiene el mismo valor (en magnitud y dirección), es homogéneo.

Un campo de fuerza se puede caracterizar líneas eléctricas. En este caso, las tangentes a las líneas de fuerza determinan la dirección de la acción de la fuerza en este campo, y la densidad de las líneas de fuerza es proporcional a la magnitud de la fuerza.

Figura: 1,23.

Central se llama fuerza, cuya línea de acción en todas las posiciones pasa por un punto determinado, llamado centro de fuerza (punto ACERCA DE en la Fig. 1,23).

El campo en el que actúa la fuerza central es el campo de fuerza central. La magnitud de la fuerza F (r), actuar sobre un mismo objeto material (punto material, cuerpo, carga eléctrica, etc.) en diferentes puntos de dicho campo, depende solo de la distancia r al centro de fuerzas, es decir

(es el vector unitario en la dirección del vector r). Todo el poder

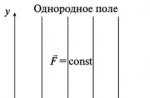
Figura: 1,24. Representación esquemática en un plano hoy campo uniforme

las líneas de dicho campo pasan por un punto (polo) O; el momento de la fuerza central en este caso con respecto al polo es idénticamente cero M 0 (F) \u003d Ç 0. Los centrales son campos gravitacionales y de Coulomb (y fuerzas, respectivamente).

La figura 1.24 muestra un ejemplo de un campo de fuerza uniforme (su proyección plana): en cada punto de dicho campo, la fuerza que actúa sobre el mismo cuerpo es la misma en magnitud y dirección, es decir,

Figura: 1,25. Representación esquemática en hoycampo no homogéneo

La figura 1.25 muestra un ejemplo de un campo no homogéneo en el que F (x,

y, z) *? const y

y no son iguales a cero 1. La densidad de las líneas de fuerza en diferentes regiones de dicho campo no es la misma: en la región de la derecha, el campo es más fuerte.

Todas las fuerzas en mecánica se pueden dividir en dos grupos: fuerzas conservadoras (que actúan en campos potenciales) y fuerzas no conservadoras (o disipativas). Las fuerzas se llaman conservador (o potencial), si el trabajo de estas fuerzas no depende ni de la forma de la trayectoria del cuerpo sobre el que actúan, ni de la longitud del camino en el área de su acción, sino que está determinado solo por la posición inicial y final de los puntos de desplazamiento en el espacio. El campo de fuerzas conservadoras se llama potencial (o conservador) campo.

Demostremos que el trabajo de las fuerzas conservadoras en un lazo cerrado es igual a cero. Para hacer esto, dividimos la trayectoria cerrada arbitrariamente en dos secciones a2 y B2 (figura 1.25). Dado que las fuerzas son conservadoras, entonces Л 1а2 \u003d А т. Por otra parte A 1b2 \u003d -A w. Entonces A ish \u003d A 1a2 + A w \u003d \u003d A a2 - A b2 \u003d 0, según sea necesario. Lo contrario también es cierto.

Figura: 1,26.

declaración: si el trabajo de las fuerzas a lo largo de un contorno cerrado arbitrario φ es igual a cero, entonces las fuerzas son conservadoras y el campo es potencial. Esta condición se escribe como una integral de contorno

Figura: 1,27.

lo que significa: en un campo de potencial, la circulación del vector F a lo largo de cualquier lazo cerrado L es igual a cero.

El trabajo de fuerzas no conservadoras en el caso general depende tanto de la forma de la trayectoria como de la longitud de la trayectoria. Un ejemplo de fuerzas no conservadoras son las fuerzas de fricción y arrastre.

Demostremos que todas las fuerzas centrales pertenecen a la categoría de fuerzas conservadoras. De hecho (figura 1.27), si la fuerza F central, entonces puede ser

1 Presentado en la fig. 1.23 el campo de fuerza central también es un campo no uniforme.

poner en la forma En este caso, el trabajo elemental de fuerza F

en desplazamiento elemental d / será o

dA \u003d F (r) dlcos а \u003d F (r) dr (desde rdl \u003d rdl cos a, a d / cos a \u003d dr). Entonces trabaja

donde f (r) es la función antiderivada.

De la expresión obtenida se desprende que la obra Ap fuerza central F depende solo del tipo de función F (r) y distancias r ( y r 2 puntos 1 y 2 del centro de fuerza O y no depende de la longitud de la trayectoria de 1 a 2, lo que refleja la naturaleza conservadora de las fuerzas centrales.

La prueba dada es general para cualquier fuerza y \u200b\u200bcampo central, por lo tanto, cubre las fuerzas mencionadas anteriormente: gravitacional y Coulomb.

Considere nuevamente un sistema cerrado que consta de dos puntos A y B. En virtud de la primera ley de Newton, si no hubiera un punto B en el sistema y el punto A estuviera libre, entonces la velocidad del punto A relativa al marco de referencia inercial no cambiaría y lo habríamos hecho.

Sin embargo, debido a la interacción de los puntos A y B, la derivada es distinta de cero. Como ya se mencionó anteriormente, la mecánica no responde a la pregunta de por qué la presencia del punto B afecta el movimiento del punto A, sino que procede del hecho de que tal efecto tiene lugar e identifica el resultado de este efecto con un vector. El impacto del punto B sobre el movimiento del punto A se llama fuerza y \u200b\u200bse dice que el punto B actúa sobre el punto A con la fuerza representada por el vector

Es esta igualdad (usando el término "fuerza") la que generalmente se llama segunda ley de Newton.

Además, el mismo punto A interactúa con varios objetos materiales. Cada uno de estos objetos, si fuera uno, provocaría la aparición de la fuerza en consecuencia. Al mismo tiempo, se postula el llamado principio de independencia de la acción de las fuerzas: la fuerza debida a cualquier fuente no depende de la presencia de fuerzas debidas a otras fuentes. Es fundamental para esto la suposición de que las fuerzas aplicadas al mismo punto pueden sumarse de acuerdo con las reglas habituales de la suma de vectores y que la fuerza obtenida de esta manera es equivalente a las originales. Debido al supuesto de independencia de la acción de las fuerzas, el conjunto de acciones aplicadas a un punto material puede ser reemplazado por una acción, representada, respectivamente, por una fuerza, que se obtiene por engomado geométrico de los vectores de todas las fuerzas que actúan.

La fuerza es el resultado de la interacción de objetos materiales. Esto significa que si se debe a la presencia del punto B, entonces, a la inversa, se debe a la presencia del punto A. La relación entre fuerzas y está establecida por el tercer postulado (ley) de Newton. Según este postulado, al interactuar entre objetos materiales, las fuerzas y son iguales en magnitud, actúan a lo largo de una línea recta, pero dirigidas a lados opuestos. Esta ley a veces se formula brevemente como sigue: "cualquier acción es igual y opuesta a la reacción".

Esta declaración es un nuevo postulado. No surge de ninguna manera de los supuestos iniciales anteriores y, en general, es posible construir mecánicas sin este postulado o con su otra formulación.

Al considerar un sistema de puntos materiales, es conveniente dividir todas las fuerzas que actúan sobre los puntos del sistema considerado en dos clases. La primera clase incluye fuerzas que surgen debido a las interacciones de puntos materiales incluidos en este sistema. Las fuerzas de este tipo se denominan internas. Las fuerzas que surgen debido al impacto en los puntos materiales del sistema en consideración por otros objetos materiales que no están incluidos en este sistema se denominan externas.

2. Trabajo de fuerza.

El producto escalar, donde es el incremento infinitamente pequeño del vector de radio cuando un punto material se desplaza a lo largo de su trayectoria, se denomina trabajo de fuerza elemental y se denota. La suma del trabajo elemental de todas las fuerzas que actúan sobre los puntos del sistema se denomina trabajo elemental de las fuerzas del sistema y se denota

Expresando los productos escalares en términos de las proyecciones de los factores en los ejes de coordenadas, obtenemos

(18)

Si las proyecciones de fuerzas y los incrementos de coordenadas se expresan en términos del mismo parámetro escalar (por ejemplo, en términos de tiempo to, en el caso de un sistema que consta de un punto, en términos de desplazamiento elemental), entonces los valores en el lado derecho de las igualdades (17) y (18) se puede representar como funciones de este parámetro, multiplicado por su diferencial, y se puede integrar sobre este parámetro, por ejemplo, sobre t en el rango de a. El resultado de la integración se denota y se denomina trabajo total de la fuerza y \u200b\u200btrabajo total de las fuerzas del sistema en el tiempo, respectivamente.

Al calcular el trabajo elemental y total de todas las fuerzas del sistema, se deben tener en cuenta todas las fuerzas, tanto externas como internas. El hecho de que las fuerzas internas sean por pares iguales y de dirección opuesta resulta insignificante, ya que el movimiento de los puntos también juega un papel en el cálculo del trabajo y, por lo tanto, el trabajo de las fuerzas internas, en general, es distinto de cero.

Considere un caso particular en el que las cantidades en el lado derecho de las igualdades (17) y (18) se pueden representar como diferenciales totales

En este caso, también es natural aceptar la notación y las definiciones introducidas anteriormente:

De las igualdades (21) y (22) se deduce que en aquellos casos en que el trabajo elemental es el diferencial total de alguna función Ф, el trabajo sobre cualquier intervalo finito depende únicamente de los valores de Ф al principio y al final de este intervalo y no depende de los valores intermedios de Ф , es decir, sobre cómo ocurrió el movimiento.

3. Campo de fuerza.

En muchos problemas de mecánica, a menudo uno tiene que lidiar con fuerzas que dependen de la posición de los puntos bajo consideración (y, quizás, del tiempo) y no dependen de sus velocidades. Por ejemplo, la fuerza puede depender de la distancia entre los puntos que interactúan. En problemas técnicos, las fuerzas provocadas por los resortes dependen de la deformación de los resortes, es decir, también de la posición en el espacio del punto o cuerpo en cuestión.

Consideremos primero el caso en el que se estudia el movimiento de un punto y, por lo tanto, solo se considera una fuerza, dependiendo de la posición del punto. En tales casos, el vector de fuerza no está asociado con el punto en el que se realiza la acción, sino con puntos en el espacio. Se supone que a cada punto del espacio, definido en un determinado marco de referencia inercial, se le asocia un factor que representa la fuerza que actuaría sobre un punto material si este último se colocara en ese punto del espacio. Por tanto, se considera convencionalmente que el espacio está "lleno" de vectores en todas partes. Este conjunto de vectores se llama campo de fuerza.

Dicen que un campo de fuerza es estacionario si las fuerzas en cuestión no dependen explícitamente del tiempo. De lo contrario, el campo de fuerza se llama inestable.

Un campo se llama potencial si existe una función escalar de las coordenadas de un punto (y, quizás, el tiempo) tal que las derivadas parciales de esta función con respecto ay son iguales a las proyecciones de la fuerza F sobre los ejes x, y, z, respectivamente:

Debido al hecho de que la fuerza F es función de un punto en el espacio, es decir, coordenadas y, quizás, tiempo, sus proyecciones también son funciones de variables.

La función, si existe, se llama función de fuerza. Por supuesto, la función de fuerza no existe para todos los campos de fuerza, y las condiciones para su existencia, es decir, las condiciones para que el campo sea potencial, no se aclaran en el curso de matemáticas y están determinadas por las igualdades

Al estudiar el movimiento de N puntos que interactúan, es necesario tener en cuenta la presencia de N fuerzas que actúan sobre ellos. En este caso, se introduce el espacio -dimensional de coordenadas de puntos. Especificar un punto en este espacio determina la ubicación de todos los N puntos materiales del sistema estudiado. A continuación, se introduce en consideración el vector -dimensional con coordenadas y se considera convencionalmente que el espacio -dimensional está en todas partes densamente lleno de tales vectores. Entonces, la asignación de un punto de este espacio dimensional determina no solo la posición de todos los puntos materiales en relación con el marco de referencia inicial, sino también todas las fuerzas que actúan sobre los puntos materiales del sistema. Tal campo de fuerza dimensional se llama potencial si hay una función de fuerza Ф de todas las coordenadas tal que

Si las fuerzas se pueden representar como la suma de dos términos

de modo que los términos satisfacen las relaciones (24) y los términos no las satisfacen, entonces se denominan fuerzas potenciales, no potenciales.

Un sistema de puntos materiales se llama conservador si hay una función de fuerza que no depende explícitamente del tiempo (el campo de fuerza es estacionario) y tal que todas las fuerzas que actúan sobre los puntos satisfacen las relaciones (24).

El trabajo elemental de las fuerzas del sistema conservador.

conviene representarlo de otra forma, expresando los productos escalares en términos de las proyecciones de los factores vectoriales (fórmula (18)). Teniendo en cuenta la existencia de la función de fuerza Ф, en virtud de (23) obtenemos

es decir, el trabajo elemental es igual al diferencial total de la función de fuerza

Así, cuando un sistema conservador se mueve, el trabajo elemental se expresa por el diferencial total de alguna función, y por lo tanto

Hipersuperficies

se llaman superficies niveladas.

En la fórmula (26), los símbolos y significan los valores de Ф en los momentos del inicio y final del movimiento. Por tanto, para cualquier movimiento del sistema, cuyo origen corresponda a un punto situado en la superficie nivelada

y el final es un punto en la superficie nivelada

el trabajo se calcula mediante la fórmula (26). En consecuencia, cuando se mueve un sistema conservador, el trabajo no depende del camino, sino solo de qué superficies del nivel comenzó y terminó el movimiento. En particular, el trabajo es cero si el movimiento comienza y termina en la misma superficie nivelada.

CAMPO DE FUERZA - una parte del espacio (limitado o ilimitado), en cada punto del corte sobre la partícula de material colocada allí, una fuerza determinada por su valor numérico y dirección, que depende únicamente de las coordenadas x, y, z este punto. Tal S. del artículo se llama. estacionario; si la fuerza del campo también depende del tiempo, entonces se llama S. p. no estacionario; si la fuerza en todos los puntos de la nave espacial tiene el mismo valor, es decir, no depende de las coordenadas ni del tiempo, se llama nave espacial. homogéneo.

Estacionario S. p. Puede ser especificado por ur-ny

dónde F x, F y, F z - la proyección de la intensidad de campo F.

Si existe tal función U (x, y, z), llamada potencia f-ción, que el trabajo elemental de las fuerzas de campo es igual al diferencial total de esta f -ción, entonces se llama S. p. potencial. En este caso, la S. p. Viene dada por una función U (x, y, z), y la fuerza F se puede definir a través de esta función por igualdades:

o ... La condición para la existencia de una función de potencia para un S. p. Dado es que

o. Al moverse en un potencial S. p. Desde el punto M 1 (x 1, y 1, z 1)exactamente M 2 (x 2, y 2, z 2) el trabajo de las fuerzas de campo está determinado por la igualdad y no depende del tipo de trayectoria a lo largo del cual se mueve el punto de aplicación de la fuerza.

Superficies U (x, y, z) \u003d const, en el que la función se mantiene constante. valor, llamado. superficies niveladas. La fuerza en cada punto del campo se dirige a lo largo de la normal al nivel de la superficie que pasa por este punto; cuando se mueve a lo largo de la superficie del nivel, el trabajo de las fuerzas de campo es cero.

Ejemplos de potencial S. p .: Campo gravitatorio homogéneo, para el cual U \u003d -mgzdónde t es la masa de una partícula que se mueve en el campo, gramo - aceleración de la gravedad (eje z dirigido verticalmente hacia arriba); Campo gravitacional newtoniano, para el cual U \u003d km / r, donde r \u003d - distancia desde el centro de atracción, k - coeficiente constante para un campo dado. En lugar de una función de potencia, como característica de un potencial S. p., Puede ingresar energía potencial P asociado con U adiccion P (x, y, z)= = -U (x, y, z). El estudio del movimiento de una partícula en un potencial S. p. (En ausencia de otras fuerzas) se simplifica significativamente, ya que en este caso existe una ley de conservación de la mecánica. energía, que permite establecer una relación directa entre la velocidad de una partícula y su posición en una partícula. desde. m. Targ. LÍNEAS ELÉCTRICAS - una familia de curvas que caracterizan la distribución espacial del campo vectorial de fuerzas; la dirección del vector de campo en cada punto coincide con la tangente a S. l. Por lo tanto, ur-ción S. l. campo vectorial arbitrario A (x, y, z) se escriben como:

Densidad de S. l. caracteriza la intensidad (magnitud) del campo de fuerza. Una región del espacio limitada por S. l. Intersección k - l. curva cerrada, llamada. tubo de potencia. S. l. Los campos de vórtice están cerrados. S. l. los campos potenciales comienzan en las fuentes del campo y terminan en sus sumideros (fuentes de signo negativo).

El concepto de S. de l. introducido por M. Faraday en el estudio del magnetismo, y luego fue desarrollado en los trabajos de J.C. Maxwell sobre electromagnetismo. Según las ideas de Faraday y Maxwell, en el espacio penetrado por S. l. eléctrico y magn. campos, hay mecánicos. tensiones correspondientes a la tensión a lo largo de S. l. y la presión a través de ellos. Matemáticamente, este concepto se expresa en Tensor de tensión de Maxwell el - magn. campos.

Junto con el uso del concepto de S. l. más a menudo solo hablan de las líneas de campo: la fuerza eléctrica. campos mi, magn. de inducción campos EN y así sucesivamente, sin hacer especiales. énfasis en la relación de estos ceros con las fuerzas.

Un campo de fuerzas es una región del espacio, en cada punto en el que se aplica una fuerza a una partícula colocada allí, que varía regularmente de un punto a otro, por ejemplo, el campo de gravedad de la Tierra o el campo de fuerzas de resistencia en un flujo de fluido (gas). Si la fuerza en cada punto del campo de fuerza no depende del tiempo, entonces dicho campo se llama estacionario... Está claro que un campo de fuerza que está estacionario en un marco de referencia puede resultar no estacionario en otro marco. En un campo de fuerza estacionario, la fuerza depende solo de la posición de la partícula.

El trabajo realizado por las fuerzas de campo cuando una partícula se mueve desde un punto. 1 exactamente 2 , en general, depende del camino. Sin embargo, entre los campos de fuerza estacionarios hay aquellos en los que este trabajo no depende del camino entre los puntos 1 y 2 ... Esta clase de campos, que posee una serie de propiedades importantes, ocupa un lugar especial en la mecánica. Procederemos al estudio de estas propiedades.

Expliquemos lo que se ha dicho utilizando el ejemplo de una fuerza de seguimiento. En la Fig. 5.4 representando el cuerpo A B C D,en el punto ACERCA DE que fuerza se aplica , invariablemente asociado con el cuerpo.

Mueva el cuerpo fuera de posición yo en posición IIdos caminos. Primero escojamos el punto ACERCA DE(Fig. 5.4a)) y gire el cuerpo alrededor del poste en un ángulo π / 2 opuesto a la dirección de rotación de la derecha. El cuerpo tomará posición A B C D".Ahora informemos al cuerpo del desplazamiento de traslación en la dirección vertical por la cantidad OO ".El cuerpo tomará posición II (A "B" C "D").Fuerza el trabajo en el perfecto desplazamiento del cuerpo desde la posición. yo en posición IIes cero. El vector de desplazamiento de polos está representado por el segmento de línea OO ".

En el segundo método, elegimos el punto Khigo. 5.4b) y gire el cuerpo alrededor del poste en un ángulo π / 2 en sentido antihorario. El cuerpo tomará posición A B C D"(Figura 5.4b). Ahora mueva el cuerpo verticalmente hacia arriba con el vector del desplazamiento del polo KK ",después de lo cual le damos al cuerpo un movimiento horizontal hacia la izquierda por la cantidad K "K".Como resultado, el cuerpo tomará la posición II,lo mismo que en la posición, fig. 5.4 y) de la Figura 5.4. Sin embargo, ahora el vector de desplazamiento del polo será diferente al del primer método, y el trabajo de la fuerza en el segundo método de mover el cuerpo desde la posición yo en posición IIes igual a A \u003d F K "K",es decir, es distinto de cero.

Definición: un campo de fuerza estacionario, en el que el trabajo de la fuerza de campo en la trayectoria entre dos puntos cualesquiera no depende de la forma de la trayectoria, sino que depende solo de la posición de estos puntos, se llama potencial, y las fuerzas mismas - conservador.

Potencialtales fuerzas energía potencial) se denomina el trabajo realizado por ellos sobre los desplazamientos del cuerpo desde la posición final a la posición inicial, pudiendo elegir la posición inicial de forma arbitraria. Esto significa que la energía potencial se determina hasta una constante.

Si no se cumple esta condición, entonces el campo de fuerza no es potencial y las fuerzas de campo se denominan ningún conservante.

En los sistemas mecánicos reales, siempre hay fuerzas cuyo trabajo es negativo durante el movimiento real del sistema (por ejemplo, fuerzas de fricción). Tales fuerzas se llaman disipativo.Son un tipo particular de fuerzas no conservadoras.

Las fuerzas conservadoras tienen una serie de propiedades notables, para cuya identificación introducimos el concepto de campo de fuerza. El campo de fuerza se llama espacio(o parte de ella), en el que una determinada fuerza actúa sobre un punto material colocado en cada punto de este campo.

Demostremos que en un campo potencial, el trabajo de las fuerzas de campo en cualquier camino cerrado es cero. De hecho, cualquier camino cerrado (figura 5.5) puede dividirse arbitrariamente en dos partes, 1a2 y 2b1... Dado que el campo es potencial, entonces, por condición ,. Por otro lado, es obvio que. por lo tanto

q.E.D.

Por el contrario, si el trabajo de las fuerzas de campo en cualquier camino cerrado es cero, entonces el trabajo de estas fuerzas en el camino entre puntos arbitrarios 1 y 2 no depende de la forma del camino, es decir, el campo es potencial. Para la prueba, tome dos caminos arbitrarios 1a2 y 1b2 (ver figura 5.5). Hagamos un camino cerrado de ellos 1a2b1... El trabajo en este camino cerrado es por condición igual a cero, es decir De aquí. Pero, por lo tanto

Así, la igualdad a cero del trabajo de las fuerzas de campo en cualquier camino cerrado es una condición necesaria y suficiente para la independencia del trabajo de la forma del camino, y puede considerarse un rasgo distintivo de cualquier campo de fuerzas potencial.

El campo de fuerzas centrales. Cualquier campo de fuerza es causado por la acción de ciertos cuerpos. Fuerza que actúa sobre una partícula Y en tal campo se debe a la interacción de esta partícula con estos cuerpos. Las fuerzas que dependen solo de la distancia entre las partículas que interactúan y que se dirigen a lo largo de una línea recta que conecta estas partículas se denominan centrales. Un ejemplo de esto último son las fuerzas gravitacionales, de Coulomb y elásticas.

La fuerza central que actúa sobre una partícula. Y desde el lado de las partículas EN, se puede presentar en forma general:

dónde f(r) es una función que depende de la naturaleza dada de la interacción solo en r - distancia entre partículas; - vector unitario que especifica la dirección del vector de radio de la partícula Y relativo a la partícula EN (figura 5.6).

Demostremos que cualquier campo estacionario de fuerzas centrales es potencialmente.

Para hacer esto, consideremos primero el trabajo de las fuerzas centrales en el caso en que el campo de fuerza es causado por la presencia de una partícula estacionaria. EN... Hay un trabajo de fuerza elemental (5.8) sobre el desplazamiento. Dado que es la proyección del vector sobre el vector, o sobre el vector de radio correspondiente (figura 5.6), entonces. El trabajo de esta fuerza a lo largo de un camino arbitrario desde el punto 1 al punto 2

La expresión resultante depende solo del tipo de función f(r), es decir, sobre la naturaleza de la interacción y sobre los valores r 1 y r 2 distancias iniciales y finales entre partículas Y y EN... No depende de la forma del camino. Esto significa que el campo de fuerza dado es potencial.

Generalicemos el resultado obtenido a un campo de fuerza estacionario causado por la presencia de un conjunto de partículas estacionarias que actúan sobre la partícula. Y con fuerzas, cada una de las cuales es central. En este caso, el trabajo de la fuerza resultante cuando la partícula se mueve Y de un punto a otro es igual a la suma algebraica del trabajo de las fuerzas individuales. Y dado que el trabajo de cada una de estas fuerzas no depende de la forma del camino, el trabajo de la fuerza resultante tampoco depende de él.

Por tanto, de hecho, cualquier campo estacionario de fuerzas centrales es potencial.

Energía potencial de una partícula. El hecho de que el trabajo de las fuerzas del campo potencial dependa únicamente de las posiciones inicial y final de la partícula permite introducir el concepto extremadamente importante de energía potencial.

Imaginemos que estamos moviendo una partícula en un campo potencial de fuerzas desde diferentes puntos. Pia un punto fijo ACERCA DE... Dado que el trabajo de las fuerzas de campo no depende de la forma del camino, su dependencia permanece solo en la posición del punto R (en un punto fijo ACERCA DE). Esto significa que este trabajo será alguna función del vector de radio del punto R... Denotando esta función, escribimos

La función se llama energía potencial de una partícula en un campo dado.

Ahora encontraremos el trabajo de las fuerzas de campo al mover una partícula desde un punto 1 exactamente 2 (figura 5.7). Dado que el trabajo no depende del camino, tomamos el camino que pasa por el punto 0. Luego, el trabajo en el camino 1 02 se puede representar como

o teniendo en cuenta (5.9)

La expresión de la derecha es la disminución * de la energía potencial, es decir, la diferencia en los valores de la energía potencial de la partícula en los puntos inicial y final del camino.

_________________

* Cambio de cualquier valor X puede caracterizarse por su aumento o disminución. Aumentando el valor X se llama la diferencia de la final ( X 2) e inicial ( X 1) valores de esta cantidad:

incremento Δ X = X 2 - X 1.

Disminución de valor X es la diferencia entre su inicial ( X 1) y final ( X 2) valores:

disminución X 1 - X 2 \u003d -Δ X,

es decir, la disminución en el valor X es igual a su incremento tomado con el signo opuesto.

El aumento y la disminución son cantidades algebraicas: si X 2 > X 1, entonces el incremento es positivo y la disminución es negativa, y viceversa.

Por lo tanto, el trabajo de campo fuerza en el camino 1 - 2 es igual a la disminución de la energía potencial de la partícula.

Obviamente, a la partícula ubicada en el punto 0 del campo siempre se le puede asignar cualquier valor preseleccionado de la energía potencial. Esto corresponde al hecho de que midiendo el trabajo, solo se puede determinar la diferencia de energías potenciales en dos puntos del campo, pero no su valor absoluto. Sin embargo, una vez que se fija el valor

energía potencial en cualquier punto, sus valores en todos los demás puntos del campo están determinados de forma única por la fórmula (5.10).

La fórmula (5.10) permite encontrar una expresión para cualquier campo de fuerzas potencial. Para ello, basta con calcular el trabajo realizado por las fuerzas de campo en cualquier camino entre dos puntos, y representarlo en forma de disminución de alguna función, que es la energía potencial.

Esto es exactamente lo que se hizo al calcular el trabajo en campos de fuerzas elásticas y gravitacionales (Coulomb), así como en un campo gravitatorio homogéneo [ver. fórmulas (5.3) - (5.5)]. Es inmediatamente evidente a partir de estas fórmulas que la energía potencial de una partícula en estos campos de fuerza tiene la siguiente forma:

1) en el campo de la fuerza elástica

2) en el campo de una masa puntual (carga)

3) en un campo de gravedad uniforme

Recalcamos una vez más que la energía potencial U es una función que se determina hasta la suma de alguna constante arbitraria. Esta circunstancia, sin embargo, es completamente insignificante, porque todas las fórmulas incluyen solo la diferencia de valores U en dos posiciones de la partícula. Por tanto, se elimina una constante arbitraria, la misma para todos los puntos del campo. En este sentido se suele omitir, lo que se hace en las tres expresiones anteriores.

Y hay una circunstancia más importante que no debe olvidarse. La energía potencial, estrictamente hablando, no debe atribuirse a una partícula, sino a un sistema de partículas y cuerpos que interactúan entre sí, provocando un campo de fuerza. Con una naturaleza dada de la interacción, la energía potencial de la interacción de una partícula con estos cuerpos depende solo de la posición de la partícula en relación con estos cuerpos.

La conexión entre energía potencial y fuerza.... Según (5.10), el trabajo de la fuerza del campo potencial es igual a la disminución de la energía potencial de la partícula, es decir, Y 12 = U 1 - U 2 = - (U 2 - U 1). Para el desplazamiento elemental, la última expresión tiene la forma dА = - dUo

F l dl \u003d - dU. (5.14)

es decir, la proyección de la intensidad de campo en un punto dado en la dirección del movimiento es igual con el signo opuesto a la derivada parcial de la energía potencial en esta dirección.

, luego usando la fórmula (5.16) podemos restaurar el campo de fuerzas.

El lugar geométrico de puntos en el espacio en el que la energía potencial U tiene el mismo significado, define la superficie equipotencial. Está claro que cada valor U corresponde a su propia superficie equipotencial.

De la fórmula (5.15) se deduce que la proyección del vector en cualquier dirección tangente a la superficie equipotencial en un punto dado es igual a cero. Esto significa que el vector es normal a la superficie equipotencial en un punto dado. Además, el signo menos en (5.15) significa que el vector se dirige hacia la energía potencial decreciente. Esto se explica en la Fig. 5.8 relacionado con el caso bidimensional; el sistema de equipotenciales se muestra aquí, y U 1 < U 2 < U 3 < … .

Las fuerzas conservadoras son fuerzas cuyo trabajo no depende de la trayectoria de la transición de un cuerpo o sistema desde la posición inicial a la final. Una propiedad característica de tales fuerzas es que el trabajo en una trayectoria cerrada es cero:

Las fuerzas conservadoras incluyen: gravedad, fuerza gravitacional, fuerza elástica y otras fuerzas.

Las fuerzas no conservadoras son fuerzas cuyo trabajo depende del camino de la transición de un cuerpo o sistema desde la posición inicial a la final. El trabajo de estas fuerzas en una trayectoria cerrada es distinto de cero. Las fuerzas no conservadoras incluyen: fuerza de fricción, fuerza de tracción y otras fuerzas.

Un campo de fuerza es un espacio físico que satisface la condición bajo la cual fuerzas que dependen de la posición de estos puntos o de la posición de los puntos y el tiempo actúan sobre los puntos de un sistema mecánico en este espacio. Campo de fuerza. cuyas fuerzas no dependen del tiempo se denomina estacionaria. Un campo de fuerza estacionario se llama potencial si existe una función que depende únicamente de las coordenadas de los puntos del sistema a través de los cuales las proyecciones de la fuerza sobre los ejes de coordenadas en cada punto del campo se expresan de la siguiente manera: X i \u003d ∂υ / ∂x i; Y i \u003d ∂υ / ∂y i; Z i \u003d ∂υ / ∂z i.

Cada punto del campo potencial corresponde, por un lado, a un cierto valor del vector de fuerza que actúa sobre el cuerpo y, por otro lado, a un cierto valor de la energía potencial. En consecuencia, debe haber una cierta conexión entre la fuerza y \u200b\u200bla energía potencial.

Para establecer esta conexión, calculemos el trabajo elemental realizado por las fuerzas de campo con un pequeño desplazamiento del cuerpo a lo largo de una dirección en el espacio elegida arbitrariamente, que denotamos con una letra. Este trabajo es igual a

donde es la proyección de la fuerza en la dirección.

Dado que en este caso el trabajo se realiza a expensas de la reserva de energía potencial, es igual a la pérdida de energía potencial en el segmento del eje:

De las dos últimas expresiones obtenemos

La última expresión da el valor promedio sobre el segmento. A

para obtener el valor en el punto, debe realizar el paso hasta el límite:

Dado que puede cambiar no solo cuando se mueve a lo largo del eje, sino también cuando se mueve en otras direcciones, el límite en esta fórmula representa la llamada derivada parcial de por:

Esta relación es válida para cualquier dirección en el espacio, en particular para las direcciones de los ejes cartesianos de coordenadas x, y, z:

Esta fórmula determina la proyección del vector de fuerza sobre los ejes de coordenadas. Si se conocen estas proyecciones, se determina el vector de fuerza en sí:

en vector de matematicas ,

donde a es una función escalar x, y, z, llamada el gradiente de este escalar se denota con el símbolo. Por tanto, la fuerza es igual al gradiente de energía potencial, tomado con el signo opuesto