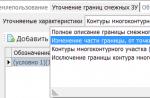
V strede v bode A.
α je uhol vyjadrený v radiánoch.

Tangenta ( opálenie α) je goniometrická funkcia závislá od uhla α medzi preponou a ramenom pravouhlého trojuholníka, ktorá sa rovná pomeru dĺžky protiľahlého ramena |BC| na dĺžku susednej nohy |AB| .

Kotangens ( ctg α) je goniometrická funkcia závislá od uhla α medzi preponou a ramenom pravouhlého trojuholníka, rovná pomeru dĺžky susedného ramena |AB| na dĺžku opačnej nohy |BC| .

Tangenta

Kde n- celý.

V západnej literatúre sa dotyčnica označuje takto:
.
;
;
.

Graf funkcie dotyčnice, y = tan x

Kotangens

Kde n- celý.

V západnej literatúre sa kotangens označuje takto:
.
Akceptované sú aj nasledujúce zápisy:
;
;
.

Graf funkcie kotangens, y = ctg x

Vlastnosti dotyčnice a kotangens

Periodicita

Funkcie y = tg x a y = ctg x sú periodické s periódou π.

Parita

Funkcie tangens a kotangens sú nepárne.

Oblasti definície a hodnôt, rastúce, klesajúce

Funkcie tangens a kotangens sú spojité vo svojej doméne definície (pozri dôkaz spojitosti). Hlavné vlastnosti tangens a kotangens sú uvedené v tabuľke ( n- celé).

	y = tg x	y = ctg x
Rozsah a kontinuita
Rozsah hodnôt	-∞ < y < +∞	-∞ < y < +∞
Zvyšovanie		-
Zostupne	-
Extrémy	-	-
Nuly, y = 0
Priesečník bodov s ordinátnou osou x = 0	y = 0	-

Vzorce

Výrazy využívajúce sínus a kosínus

; ;
; ;
;

Vzorce pre tangens a kotangens zo súčtu a rozdielu

Zostávajúce vzorce sa dajú ľahko získať napr

Súčin dotyčníc

Vzorec pre súčet a rozdiel dotyčníc

Táto tabuľka predstavuje hodnoty dotyčníc a kotangens pre určité hodnoty argumentu.

Výrazy využívajúce komplexné čísla

Vyjadrenia prostredníctvom hyperbolických funkcií

;
;

Deriváty

; .

.
Derivácia n-tého rádu vzhľadom na premennú x funkcie:
.
Odvodenie vzorcov pre dotyčnicu > > > ; pre kotangens >> >

Integrály

Rozšírenia série

Ak chcete získať rozšírenie tangens v mocninách x, musíte vziať niekoľko členov expanzie v mocninnom rade pre funkcie hriech x A cos x a rozdeliť tieto polynómy navzájom, . Takto sa získajú nasledujúce vzorce.

o .

na .
Kde Bn- Bernoulliho čísla. Určujú sa buď zo vzťahu opakovania:
;
;
Kde .
Alebo podľa Laplaceovho vzorca:

Inverzné funkcie

Inverzné funkcie tangens a kotangens sú arkustangens a arkotangens.

Arctangens, arctg

, Kde n- celý.

Arckotangens, arcctg

, Kde n- celý.

Referencie:
I.N. Bronstein, K.A. Semendyaev, Príručka matematiky pre inžinierov a vysokoškolských študentov, „Lan“, 2009.
G. Korn, Príručka matematiky pre vedcov a inžinierov, 2012.

, [−5π/2; −3π/2],. . . - jedným slovom na všetkých segmentoch [−π/2 + 2πk; π/2 + 2πk], kde k Z, a klesá na všetkých segmentoch

[π/2 + 2πn; 3π/2 + 2πn], kde n Z.

Problém 11.6. Na ktorých segmentoch sa funkcia y = cos x zvyšuje a na ktorých klesá?

Problém 11.8. Usporiadajte vzostupne: hriech 1, cos 2, sin 3, cos 4, sin 5, cos 6.

§ 12. Grafy tangens a kotangens

Nakreslíme funkciu y = tan x. Najprv ho zostrojme pre čísla x patriace do intervalu (−π/2; π/2).

Ak x = 0, potom tan x = 0; keď sa x zvýši z 0 na π/2, zväčší sa aj tan x – to je možné vidieť, ak sa pozriete na os dotyčnice (obr. 12.1 a). Keď sa x blíži k π/2, zostáva menšie

Ryža. 12.2. y = tan x.

π/2, hodnota tan x narastá (bod M na obr. 12.1 a stúpa stále vyššie) a môže sa samozrejme stať ľubovoľne veľkým kladným číslom. Podobne, keď x klesá z 0 na −π/2, tan x sa stáva záporným číslom, ktorého absolútna hodnota sa zvyšuje, keď sa x blíži k −π/2. Pre x = π/2 alebo −π/2 nie je funkcia tan x definovaná. Preto graf y = tan x pre x (−π/2; π/2) vyzerá približne ako na obr. 12,1 b.

V blízkosti začiatku súradníc je naša krivka blízko priamky y = x x: koniec koncov, pre malé ostré uhly platí približná rovnosť tg x ≈ x. Môžeme povedať, že priamka y = x sa dotýka grafu funkcie y = tan x v počiatku. Okrem toho krivka na obr. 12.1 b je symetrická podľa začiatku. Vysvetľuje sa to tým, že funkcia y = tan x je nepárna, teda platí identita tg(−x) = −tan x.

Ak chcete vykresliť funkciu y = tan x pre všetky x, nezabudnite, že tan x je periodická funkcia s periódou π. Preto, aby sme získali úplný graf funkcie y = tan x, je potrebné krivku na obr opakovať nekonečne veľakrát. 12.1 b, posúvajúc ho po úsečke do vzdialeností πn, kde n je celé číslo. Konečný pohľad na graf funkcie y = tan x je na obr. 12.2.

Podľa grafu opäť vidíme, že funkcia y = tan x

Ryža. 12.3. y = detská postieľka x.

nie je definovaná pre x = π/2 + πn, n Z, teda pre tie x, pre ktoré cos x = 0. Zvislé čiary s rovnicami x = π/2, 3π/2,. . . , ku ktorému sa vetvy prístupu grafu nazývajú asymptoty grafu.

Na rovnakom obr. 12.2 sme znázornili riešenia rovnice tg x = a.

Nakreslíme funkciu y = detská postieľka x. Najjednoduchším spôsobom je použiť redukčný vzorec ctg x = tan(π/2 − x) na získanie tohto grafu z grafu funkcie y = tan x pomocou transformácií podobných tým, ktoré sme opísali v predchádzajúcom odseku. Výsledok je znázornený na obr. 12.3

Problém 12.1. Graf funkcie y = ctg x získame z grafu funkcie y = tan x pomocou symetrie okolo určitej priamky. Ktorý? Existujú ďalšie linky s touto vlastnosťou?

Problém 12.2. Ako vyzerá rovnica priamky dotyčnice ku grafu funkcie y = cot x v bode so súradnicami (π/2; 0)?

Problém 12.3. Porovnajte čísla: a) tg(13π/11) a tg 3,3π; b) tan 9,6π a detská postieľka (−11,3π).

Problém 12.4. Usporiadajte čísla vo vzostupnom poradí: tg 1, tg 2, tg 3, tg 4, tg 5.

Problém 12.5. Graf funkcií:

a) y = tan(2x − π/3);	b) y = 2 postieľky (π/4 − x).
Problém 12.6. Graf funkcií:
a) y = arctan x;	b) y = arcctg x.

Problém 12.7. Nakreslite funkciu y = arctan x + arctan(1/x).

§ 13. Čomu sa rovná hriech x + cos x?

V tejto časti sa pokúsime vyriešiť nasledujúci problém: akú najväčšiu hodnotu môže mať výraz sin x + cos x?

Ak ste počítali správne, mali by ste zistiť, že zo všetkých x uvedených v tejto tabuľke je najväčšia hodnota sin x + cos x

sa získa pre x blízke 45◦ alebo, v radiánovej miere, k π/4.

Ak x = π/4, presná hodnota sin x+cos x je 2. Ukazuje sa, že náš experimentálny výsledok a

je vlastne pravda: pre všetky x platí nerovnosť sin x + cos x 6

2, takže 2 je najväčšia hodnota akceptovaná týmto výrazom.

Zatiaľ nemáme dostatok prostriedkov, aby sme túto nerovnosť dokázali tým najprirodzenejším spôsobom. Zatiaľ si ukážeme, ako to zredukovať na problém planimetrie.

Ak 0< x < π/2, то sin x и cos x - катеты прямоугольного треугольника с гипотенузой 1 и острым углом x (рис. 13.1 ).

Preto je naša úloha preformulovaná nasledovne: dokázať, že súčet dĺžok ramien pravouhlého trojuholníka s preponou 1 bude maximálny, ak je tento trojuholník rovnoramenný.

Problém 13.1. Dokážte toto tvrdenie.

Keďže rovnoramenný pravouhlý trojuholník s hy-

Potenuse 1, súčet dĺžok nôh je rovný 2√, výsledok tejto úlohy implikuje nerovnosť sin x + cos x 6 2 pre všetky x ležiace v intervale (0; π/2). Odtiaľto nie je ťažké vyvodiť záver, že táto nerovnosť vo všeobecnosti platí pre všetky x.

Výsledok úlohy 13.1 neplatí len pre pravouhlé trojuholníky.

Problém 13.2. Dokážte, že spomedzi všetkých trojuholníkov s danými hodnotami strany AC a uhla B bude najväčší súčet AB + BC pre rovnoramenný trojuholník so základňou AC.

Vráťme sa k trigonometrii.

Problém 13.3. Pomocou tabuľky sínusov z § 3 zostrojte bod po bode graf funkcie y = sin x + cos x.

Poznámka: Pamätajte, že x musí byť vyjadrené v radiánoch; Pre hodnoty x mimo intervalu použite redukčné vzorce.

Ak ste urobili všetko správne, mali by ste mať krivku, ktorá vyzerá ako sínusoida. Neskôr uvidíme, že táto krivka nie je len podobná, ale je to sínusoida. Naučíme sa tiež nájsť najväčšie hodnoty výrazov ako 3 sin x + 4 cos x (mimochodom, graf funkcie y = 3 sin x + 4 cos x je tiež sínusoida!).

Tento video tutoriál pojednáva o vlastnostiach funkcií y =tgx, y = ctgX, ukazuje, ako zostaviť ich grafy.

Videonávod začína pohľadom na funkciu y =tgX.

Vlastnosti funkcie sú zvýraznené.

1) Oblasť definície funkcie y =tgX volajú sa všetky reálne čísla, okrem x =π/2 + 2 πk. Tie. na grafe nie sú žiadne body, ktoré by patrili k čiare x =π/2 a x = -π/2, ako aj x = 3π/2 a tak ďalej (s rovnakou periodicitou). Takže graf funkcie y =tgX bude pozostávať z nekonečného počtu vetiev, ktoré sa budú nachádzať v priestoroch medzi priamkami x = - 3π/2 a x = -π/2 , x = -π/2 a x = π/2 a tak ďalej.

2) Funkcia y =tgX je periodické, kde hlavná perióda je π. To potvrdzuje rovnosť tg(x- π ) = tg x =tg(x+π ) . Tieto rovnosti boli študované skôr, autor vyzýva študentov, aby si ich pripomenuli, pričom poukazuje na to, že pre akúkoľvek platnú hodnotu t platí rovnosť:

tg(t+ π ) = tg t a c tg(t+π ) = ctg t. Dôsledkom týchto rovníc je, že ak jedna vetva grafu funkcie y = tan X medzi riadkami X = - π/2 a X= π/2, potom zostávajúce vetvy možno získať posunutím tejto vetvy pozdĺž osi x o π, 2π a tak ďalej.

3) Funkcia y =tgX je zvláštne, pretože . tg (- x) =- tg x.

Ďalej prejdime ku konštrukcii grafu funkcie y =tgX. Ako vyplýva z vlastností funkcie opísanej vyššie, funkcia y =tgX periodické a nepárne. Stačí teda zostrojiť časť grafu – jednu vetvu v jednom intervale a následne použiť na prenos symetriu. Autor poskytuje tabuľku, v ktorej sú vypočítané hodnoty tgX pri určitých hodnotách X pre presnejšie vykresľovanie. Tieto body sú vyznačené na súradnicovej osi a spojené hladkou čiarou. Pretože Ak je graf symetrický vzhľadom na počiatok súradníc, potom je zostrojená rovnaká vetva, symetrická vzhľadom na počiatok súradníc. V dôsledku toho dostaneme jednu vetvu grafu y =tgX. Potom pomocou posunu pozdĺž osi x o π, 2 π atď. sa získa graf y =tgX.

Graf funkcie y =tgX sa nazýva tangentoid a tri vetvy grafu znázornené na obrázku sú hlavnými vetvami tangentoidu.

4) Funkcia y =tgX v každom z intervalov (- + ; +) sa zvyšuje.

5) Graf funkcií y =tgX nemá žiadne obmedzenia nad ani pod.

6) Funkcia y =tgX nemá najväčšiu a najmenšiu hodnotu.

7) Funkcia y =tgX nepretržite v akomkoľvek intervale (- - π/2+π;π/2+π). Priamka π/2+π sa nazýva asymptota grafu funkcie y =tgX, pretože v týchto bodoch je graf funkcie prerušený.

8) Sada funkčných hodnôt y =tgX volajú sa všetky reálne čísla.

Ďalej vo videonávode je uvedený príklad: vyriešte rovnicu s tgX. Na vyriešenie zostrojíme 2 grafy funkcie pri a nájdite priesečníky týchto grafov: toto je nekonečná množina bodov, ktorých úsečky sa líšia o πk. Koreň tejto rovnice bude X= π/6 +πk.

Zvážte graf funkcie y =ctgX. Funkciu je možné zobraziť v grafe dvoma spôsobmi.

Prvá metóda zahŕňa vytvorenie grafu podobne ako zostrojenie grafu funkcie y =tgX. Zostavme jednu vetvu funkčného grafu y = ctgX medzi riadkami X= 0u X= π. Potom pomocou symetrie a periodicity zostrojíme ďalšie vetvy grafu.

Druhá metóda je jednoduchšia. Graf funkcie y = сtgx možno získať transformáciou dotyčníc pomocou redukčného vzorca stgx = - tg(x +π/2). Aby sme to dosiahli, posuňme jednu vetvu funkčného grafu y = tgx pozdĺž osi x o π/2 doprava. Zostávajúce vetvy sa získajú posunutím tejto vetvy pozdĺž osi x o π, 2π atď. Graf funkcie y = ctg X sa nazýva aj tangentoid a vetva grafu v intervale (0;π) je hlavnou vetvou tangentoidu.

DEKODOVANIE TEXTU:

Zvážime vlastnosti funkcie y = tan x (y sa rovná dotyčnici x), y = ctg x (y sa rovná kotangensu x) a zostrojíme ich grafy. Zvážte funkciu y = tgx

Pred vykreslením funkcie y = tan x si zapíšme vlastnosti tejto funkcie.

VLASTNOSŤ 1. Definičný obor funkcie y = tan x sú všetky reálne čísla, okrem čísel v tvare x = + πk (x sa rovná súčtu pi nad dvoma a pi ka).

To znamená, že na grafe tejto funkcie nie sú žiadne body, ktoré patria do priamky x = (dostaneme, ak k = 0 ka sa rovná nule) a priamka x = (x sa rovná mínus pi o dve) (my dostaneme, ak k = - 1 ka sa rovná mínus jedna) a priamka x = (x sa rovná trom pi x dva) (dostaneme, ak k = 1 sa rovná jednej) atď. To znamená, že graf funkcie y = tan x bude pozostávať z nekonečného počtu vetiev, ktoré sa budú nachádzať v intervaloch medzi priamkami. Konkrétne v pásme medzi x = a x =-; v páse x = - a x = ; v páse x = a x = a tak ďalej do nekonečna.

VLASTNOSŤ 2. Funkcia y = tan x je periodická s hlavnou periódou π. (Keďže dvojitá rovnosť je pravdivá

tan(x- π) = tanx = tan (x+π) dotyčnica x mínus pi sa rovná dotyčnici x a rovná sa dotyčnici x plus pi). Túto rovnosť sme zvážili pri štúdiu tangens a kotangens. Pripomeňme mu:

Pre akúkoľvek prípustnú hodnotu t platia rovnosti:

tg (t + π) = tgt

ctg (t + π) = ctgt

Z tejto rovnosti vyplýva, že po zostrojení vetvy grafu funkcie y = tan x v intervale od x = - a x = získame zvyšné vetvy posunutím zostrojenej vetvy pozdĺž osi X o π, 2π , a tak ďalej.

VLASTNOSŤ 3. Funkcia y = tan x je nepárna funkcia, pretože rovnosť tg (- x) = - tan x je pravdivá.

Nakreslíme funkciu y = tg x

Keďže táto funkcia je periodická, pozostáva z nekonečného počtu vetiev (v páse medzi x = a x =, ako aj v páse medzi x = a x = atď.) a nepárnych, zostrojíme časť graf bod po bode v intervale od nuly do pi po dvoch (), potom použite symetriu pôvodu a periodicity.

Zostavme tabuľku dotyčnicových hodnôt na vykreslenie.

Nájdeme prvý bod: s vedomím, že pri x = 0 tan x = 0 (x sa rovná nule, tan x sa tiež rovná nule); ďalší bod: v x = tan x = (x sa rovná pi x šesť, dotyčnica x sa rovná odmocnine tri x tri); Všimnime si nasledujúce body: pri x = tan x = 1 (x sa rovná pi x štyri tan x sa rovná jednej) a x = tg x = (x sa rovná pi x tri tan x sa rovná druhej odmocnine z troch). Získané body označte na súradnicovej rovine a spojte ich hladkou čiarou (obr. 2).

Keďže graf funkcie je symetrický vzhľadom na počiatok súradníc, zostrojíme rovnakú vetvu symetricky vzhľadom na počiatok súradníc. (obr. 3).

A nakoniec, použitím periodicity, získame graf funkcie y = tan x.

Zostrojili sme vetvu grafu funkcie y = tan x v páse z x = - a x =. Zvyšné vetvy postavíme posunutím zostrojenej vetvy pozdĺž osi X o π, 2π atď.

Vytvorený graf sa nazýva tangentoid.

Časť tangentoidu znázornená na obrázku 3 sa nazýva hlavná vetva tangentoidu.

Na základe grafu si zapíšeme ešte niektoré vlastnosti tejto funkcie.

VLASTNOSŤ 4. Funkcia y = tan x sa zvyšuje na každom z intervalov (od mínus pi o dva plus pi ka po pi o dva plus pi ka).

VLASTNOSŤ 5. Funkcia y = tan x nie je ohraničená ani nad, ani pod.

VLASTNOSŤ 6. Funkcia y = tan x nemá najväčšie ani najmenšie hodnoty.

VLASTNOSŤ 7. Funkcia y = tan x je spojitá na ľubovoľnom intervale tvaru (od mínus pi krát dva plus pi ka po pi krát dva plus pi ka).

Priamka tvaru x = + πk (x sa rovná súčtu pi nad dvoma a pi ka) je zvislou asymptotou grafu funkcie, keďže v bodoch tvaru x = + πk funkcia trpí a diskontinuita.

VLASTNOSŤ 8. Množina hodnôt funkcie y = tan x sú všetky reálne čísla, to znamená (e z eff sa rovná intervalu od mínus nekonečna do plus nekonečna).

PRÍKLAD 1. Vyriešte rovnicu tg x = (dotyčnica x sa rovná odmocnine tri krát tri).

Riešenie. Zostrojme grafy funkcií y = tan x v jednom súradnicovom systéme

(y sa rovná dotyčnici x) a y = (y sa rovná odmocnine troch delené tromi).

Získali sme nekonečne veľa priesečníkov, ktorých úsečka sa od seba líšia o πk (pi ka), keďže tg x = v x =, úsečka priesečníka na hlavnej vetve sa rovná (pi o šesť).

Všetky riešenia tejto rovnice zapíšeme vzorcom x = + πk (x sa rovná pi krát šesť plus pi ka).

Odpoveď: x = + πk.

Zostavme graf funkcie y = сtg x.

Zoberme si dva spôsoby výstavby.

Prvý spôsob je podobný vykresleniu funkcie y = tan x.

Keďže táto funkcia je periodická, pozostáva z nekonečného počtu vetiev (v pásme medzi x = 0 a x =π, ako aj v pásme medzi x =π a x = 2π atď.) a nepárnych, zostrojíme časť grafu bod po bode na intervale od nuly do pi po dvoch (), potom použijeme symetriu a periodicitu.

Na zostavenie grafu použijeme tabuľku kotangensových hodnôt.

Označte výsledné body na rovine súradníc a spojte ich hladkou čiarou.

Keďže graf funkcie je relatívne symetrický, zostrojíme rovnakú vetvu symetricky.

Aplikujme periodicitu a získajme graf funkcie y = сtg x.

Zostrojili sme vetvu grafu funkcie y = сtg x v páse z x = 0 a x =π. Zvyšné vetvy zostrojíme posunutím zostrojenej vetvy pozdĺž osi x o π, - π, 2π, - 2π atď.

Druhý spôsob vykreslenie funkcie y =сtg x.

Najjednoduchší spôsob, ako získať graf funkcie y =сtg x, je transformovať dotyčnicu pomocou redukčného vzorca (kotangens x sa rovná mínus dotyčnici súčtu x a pi o dve).

V tomto prípade najprv posunieme vetvu grafu funkcie y =tg x pozdĺž osi x doprava, dostaneme

y = tg (x+) a potom vykonáme symetriu výsledného grafu vzhľadom na os x. Výsledkom bude vetva grafu funkcie y =сtg x (obr. 4). Keď poznáme jednu vetvu, môžeme zostaviť celý graf pomocou periodicity funkcie. Zvyšné vetvy zostrojíme posunutím zostrojenej vetvy pozdĺž osi x o π, 2π atď.

Graf funkcie y =сtg x sa tiež nazýva tangentoid, rovnako ako graf funkcie y =tg x. Vetva, ktorá leží v intervale od nuly do pi, sa nazýva hlavná vetva grafu funkcie y = сtg x.