Definición. La ecuación característica de un operador lineal f es una ecuación de la forma, donde λ es cualquier número real, A es la matriz del operador lineal, E es la matriz unitaria del mismo orden.
Polinomio llamado polinomio característico matriz A (operador lineal f). En forma de matriz, la ecuación característica es la siguiente:
o
.
Por lo tanto, igualando el polinomio característico a cero, obtenemos una ecuación de grado norte, donde λ es la incógnita, obtenemos los valores de sus raíces, los números característicos de la matriz dada. Las raíces características juegan un papel importante en muchas áreas de las matemáticas. Considere una de las aplicaciones de las raíces características, una herramienta muy importante en el estudio de espacios lineales, así como en la resolución de muchos problemas aplicados de álgebra lineal.
El conjunto de todas las raíces de la ecuación característica se llama espectro del operador F(cada raíz se considera con la multiplicidad que tiene en la ecuación característica).
Ejemplo. Encuentra las raíces características de la matriz.
Compongamos la matriz
Igualando el polinomio característico a cero, obtenemos la ecuación cuadrática
Entonces las raíces de la ecuación son 
.
Definición. Sea f un operador lineal del espacio y un vector distinto de cero para el cual la igualdad
donde es un número real. Entonces, el vector se llama autovector del operador y matriz de su definición, el autovalor o autovalor de la transformación. Se dice que el vector propio se refiere al valor propio.
Los autovectores juegan un papel importante tanto en las matemáticas como en sus aplicaciones. Por ejemplo, resonancia, en la que las frecuencias naturales de las oscilaciones del sistema coinciden con la frecuencia de las oscilaciones de las fuerzas externas. En matemáticas, los vectores propios son útiles para resolver sistemas de ecuaciones diferenciales.
Teorema. Si el operador lineal f en la base (la primera base) tiene la matriz A y en la base (la segunda base), la matriz B, entonces la igualdad se cumple :.
En consecuencia, al pasar a una nueva base, el polinomio característico del operador lineal no cambia.
◌ Si T es la matriz de transición de la primera base a la segunda, entonces. Luego transformamos el lado derecho de la igualdad ●
Teorema... Para que el número λ 0 del campo P sea un valor propio del vector del espacio L n sobre P, es necesario y suficiente que el número λ 0 sea la raíz característica del operador f.
Doc. I. Necesitar. Permitir λ 0 valor propio del operador F, luego en L n hay un vector propio tal que.
Permitir 
¿Es su línea de coordenadas de alguna manera, entonces
Por otro lado, desde , donde es la matriz del operador lineal en una base dada, entonces
Igualando los lados derechos (1) y (2) obtenemos:
(3)
Igualdades (3) significan que un vector numérico con coordenadas 
es una solución al siguiente sistema de ecuaciones (4).
(4)
El vector es diferente de cero (ya que es adecuado), por lo tanto, el sistema (4) tiene una solución distinta de cero, por lo que su determinante es igual a 0.
(5)
y, por tanto, el determinante transpuesto es igual a 0.
(6)
Por lo tanto, λ 0 Es la raíz de la ecuación característica.
II. Adecuación. Permitir λ 0
Es la raíz característica del operador de alguna manera 
... Demostremos que λ 0
es el valor propio del operador A.
De hecho, si λ 0 Si es la raíz característica, entonces se mantendrá la igualdad (6) y, por lo tanto, la igualdad (5), y esto significará que el sistema (4) tiene soluciones distintas de cero.
Elijamos alguna solución distinta de cero del sistema (4): el vector numérico 
... Entonces se mantienen las igualdades (3).
Considere un vector, y para él se mantendrá la igualdad (2) y, en virtud de la fórmula, la igualdad (1) es verdadera, donde es la matriz del operador en la base V... Esto implica igualdad, lo que significa que el vector es un vector propio del operador, que corresponde al valor propio λ 0 ... Esto era lo que se requería demostrar. Se demuestra el teorema.
Comentario. Para encontrar los valores propios del operador, es necesario componer y resolver la ecuación (5). Para encontrar los vectores propios del operador, es necesario componer el sistema de ecuaciones (4) y encontrar el conjunto fundamental de soluciones de este sistema.
Para controlar la exactitud del cálculo de los valores propios (pueden ser coincidentes, complejos), se utilizan dos hechos:
1) 
, donde la última suma de la traza de la matriz es la suma de los elementos diagonales.
2) 
.
Ejemplo. Encuentre autovalores y autovectores 
.
Igualando a cero obtenemos. ...
3) . , 
.
Sea una variable libre, entonces obtenemos un vector 
.
El ejercicio. Verifique el vector.
.
La ecuación característica es:
Para determinar el tipo de componente libre, es necesario componer y resolver la ecuación característica: z (p) = 0. Para escribir la ecuación característica, es necesario dibujar un diagrama en el que se deben reemplazar todas las fuentes de EMF y corriente. por su propia resistencia interna, y la resistencia de inductancia y capacitancia debe tomarse respectivamente igual a Pl y, además, es necesario romper cualquier rama de este circuito, anotar su resistencia inicial en relación con los puntos de ruptura, igualarla a cero, Resuelva y determine las raíces de p, si las raíces resultaron ser realmente negativas, entonces el componente libre de la función deseada:
, donde m es el número de raíces de la ecuación;
Raíces; -integrable permanente.
Si las raíces de la ecuación del carácter resultan ser conjugadas complejas, entonces el estado libre tendrá la forma:
donde esta la frecuencia de vibraciones libres;
La fase inicial de vibraciones libres.
8. Tiempo transitorio. Determinación de prácticamente t pp. Cálculo del tiempo del proceso transitorio.
El tiempo del proceso transitorio depende del coeficiente de amortiguamiento, el valor inverso se llama constante de tiempo y representa el tiempo durante el cual el valor del componente libre del proceso transitorio disminuirá en un factor de e = 2.72. El valor depende del circuito y los parámetros. Por lo tanto, para un circuito con conexión en serie r y L =, y para una conexión en serie
95% final del transitorio 3.
Las curvas de los componentes libres del proceso transitorio se construyen más fácilmente estableciendo los valores de tiempo t 0 ,, 2 ... .. Si hay varias raíces reales, entonces la curva resultante se obtiene sumando las ordenadas de términos (Fig. 1.)
Foto 1:
9.10, Proceso transitorio en r, C - circuito cuando se conecta a una fuente de voltaje constante. Realizar el análisis utilizando el método clásico; dar expresiones analíticas para U C (t); i C (t); gráficos. (Método clásico).
La ecuación de estado del circuito rC después de la conmutación es la siguiente:
(1) o rC (2)
Su solución: 
La capacitancia C, después de que la llave se cierra en t, se cargará a un valor de estado estable.
Dado que las condiciones iniciales son cero, según la ley de conmutación 
para t = 0, o 0 = A, de donde A = -E.
La solución a la ecuación (2) tomará la forma:
Corriente del circuito i (t) = C
Foto 1.
Figura 2.
Los gráficos de los cambios en el voltaje y la corriente i (t) se muestran en las Figuras 1 y 2. Se puede ver en las figuras que el voltaje a través del capacitor aumenta exponencialmente de 0 a E, mientras que la corriente en el momento de la conmutación alcanza abruptamente el valor de E / r, y luego disminuye hasta cero.
11.12 Proceso transitorio en r, C - circuito cuando se conecta a una fuente de voltaje sinusoidal. Realizar el análisis utilizando el método clásico; dar expresiones analíticas para U C (t); i C (t); gráficos. (Método clásico).
La ecuación de estado del circuito rC en el modo transitorio es la siguiente
rC 
.
Solución a esta ecuación:
Componente libre
donde = rC
Dado que el circuito es lineal, entonces con una acción sinusoidal y en un estado estable, el voltaje a través del capacitor también cambiará de acuerdo con una ley sinusoidal con la frecuencia de la acción de entrada. Por lo tanto, para determinar =, usaremos el método de amplitudes complejas:
; 
Considerando que j =, obtenemos:
Constante de integración A del componente libre
Hallemos de las condiciones iniciales en el circuito, teniendo en cuenta la ley de conmutación:
. Para t = 0, la última expresión tiene la forma
De donde A = -
Sumando los componentes y, obtenemos la expresión final para el voltaje a través del capacitor en el modo transitorio:
= + = 
- (1)
El análisis de la expresión (1) muestra que el proceso transitorio en el circuito rC bajo acción sinusoidal depende de la fase inicial de la fuente EMF en el momento de la conmutación y de la constante de tiempo del circuito rC.
Si, entonces = 0 y en el circuito inmediatamente después de la conmutación vendrá un estado estable, es decir
A voltaje = -, es decir el voltaje a través del capacitor inmediatamente después de la conmutación puede alcanzar casi el doble del valor del signo positivo, y luego gradualmente acercarse a =.
La diferencia de fase traerá la ecuación (1) a la forma:
La diferencia entre este modo y el anterior es que el voltaje a través del capacitor inmediatamente después de la conmutación puede alcanzar casi el doble del valor del signo negativo.
Para el circuito Rc considerado con una fuente de corriente sinusoidal en el modo de estado estable, la fase inicial del voltaje de entrada no juega ningún papel, pero su influencia es significativa en el proceso transitorio.
13. Proceso transitorio en circuitos r, L, C cuando se conecta a una fuente de voltaje constante. Proceso periódico. Expresiones analíticas para i (t), gráficas. (Método clásico).
Las raíces son reales, negativas, diferentes.
Yo (t) = Yo configuro + A1e p 1 t + A2e p 2 t
El proceso es periódico:
t = 0 (i (0) = A1 + A2; A1 = -A2
{ 
t = 0 yo l (0) * r + L + Uc (0) = E A1 = -A2 = ()
yo l (t) = ( 
)
14. Proceso transitorio en circuitos r, L, C cuando se conecta a una fuente de voltaje constante. Proceso crítico. Expresiones analíticas para i (t), gráficas. (Método clásico).
yo l (t) = yo configuro + (B1 + B2 * t) *
t = 0: yo l (0) = β1 = 0
Si las raíces son reales, negativas, iguales, entonces el proceso es crítico.
15. Proceso transitorio en r, L, C - circuito cuando se conecta a una fuente de voltaje constante. Proceso oscilatorio. Expresión analítica para i (t), gráficas. (Método clásico).
P t = -δ ± j * ω sv ω sv =
Raíces reales negativas, conjugado parcialmente complejo.
yo l (t) = yo boca A1e - δt * sin (ω sv t + ψ)
yo l (t) = yo boca + (M * cos ω sv t + N * sin ω sv t) *
yo l (t) = * 
= *
16. Proceso transitorio en r, L, C - circuito cuando se conecta a una fuente de voltaje sinusoidal. Proceso aperiódico. Expresión analítica para i (t), gráficas. (Método clásico).
R (t) = E máx * sin (ωt + ψ)
2. 
En el caso clásico, el número de ecuaciones en este caso es igual al número de ramas del circuito.
método, la solución se encuentra en la forma de la suma de las soluciones general y particular. El cálculo del proceso transitorio se describe mediante un sistema de ecuaciones diferenciales ordinarias compilado por uno de los métodos de cálculo para valores instantáneos de funciones de tiempo. La solución para cada variable de este sistema se encuentra como la suma de las soluciones general y particular. Para componer la ecuación se puede utilizar lo siguiente: un método basado en la aplicación de las leyes de Kirchhoff, un método de potenciales nodales, un método de corrientes de lazo, etc. Por ejemplo, un sistema de ecuaciones diferenciales, compilado después de cambiar de acuerdo con la primera y segunda leyes de Kirchhoff, tiene la forma:
Por ejemplo,
El número de ecuaciones en este caso es igual al número de ramas del circuito. Supongamos que se requiere encontrar la corriente i k en la rama con el número K. Excluyendo las corrientes de las ramas en sucesión, obtenemos como resultado la corriente i k y sus derivadas hasta el orden de n:
El orden de la ecuación diferencial n está determinado por el número de elementos del circuito reactivo independientes (m). Normalmente n = m, pero dependiendo del método de conexión, puede ser que n Los elementos capacitivos conectados en serie se pueden reemplazar con un elemento, al igual que los elementos inductivos conectados en paralelo se pueden reemplazar con uno equivalente. La figura 9.5 muestra la sustitución de 2 tanques en serie por uno equivalente. En el caso general, el orden de la ecuación diferencial n es: n = n lc -n ce -n lj, donde n lc es el número de elementos reactivos (L y C) en el circuito, n ce es el número de capacitivos circuitos, n lj es el número de nodos inductivos o secciones. Capacitivo significa un circuito que consta de elementos capacitivos o elementos capacitivos y fuentes ideales de EMF, Figura 9.6.a. Inductivo significa un nodo en el cual las ramas inductivas o las ramas inductivas y las fuentes de corriente convergen (Figura 9.6.b), o secciones que solo cruzan inductivas ramas o ramas inductivas y fuentes de corriente. Tenga en cuenta que la etapa de elaboración de la ecuación diferencial no es obligatoria y la corriente o tensión transitorias se pueden encontrar sin elaborar la ecuación. Como se indicó, en el método clásico para calcular procesos transitorios, la solución de ecuaciones Una solución particular describe un régimen llamado forzado. La solución de la ecuación homogénea (el lado derecho es igual a cero) describe el proceso en ausencia de EMF externos y fuentes de corriente y se llama libre. En consecuencia, se consideran corrientes, tensiones y cargas libres y forzadas. Por lo tanto, la corriente en la rama con el número K se representa como una suma. ) A = ||un ik||norte 1 restando λ de los elementos diagonales. Este determinante es un polinomio con respecto a X, el polinomio característico. En el formulario abierto H. y. escrito así: dónde S 1 = a 11 + a 22 +...
Ana- así llamado. rastro de matriz, S 2- la suma de todos los menores mayores de segundo orden, es decir, menores de la forma i k), etc., y S norte- determinante de matriz A... Raíces H. y. λ 1, λ 2, ..., λ norte se llaman valores propios de la matriz A... Para una matriz simétrica real, así como para una matriz hermitiana, todos los λ k son reales, para una matriz simétrica sesgada real todos λ k números puramente imaginarios; en el caso de una matriz ortogonal real, así como una matriz unitaria, todos | λ k| = 1. H. y. se encuentran en las más diversas áreas de las matemáticas, la mecánica, la física, la tecnología. En astronomía, al determinar las perturbaciones seculares de los planetas, también llegan a H. y.; de ahí el segundo nombre de H. y. - ecuación secular. 2) H. y. ecuación diferencial lineal con coeficientes constantes un 0λ y (norte) + a 1 año (n-1) +... + a n-1 y " + alguna = 0 Una ecuación algebraica que se obtiene a partir de una ecuación diferencial dada después de reemplazar la función a y sus derivadas por las potencias correspondientes de λ, es decir, la ecuación un 0λ norte + un 1λ n-1 +
... +
un n-1 y " + alguna = 0. Se llega a esta ecuación cuando se busca una solución particular de la forma a = Mirad λ NS para una ecuación diferencial dada. Para un sistema de ecuaciones diferenciales lineales H. y. escrito usando un calificador H. y. matrices A = Gran enciclopedia soviética. - M.: Enciclopedia soviética.
1969-1978
.
En muchos casos, los procesos físicos que ocurren en sistemas se describen mediante un sistema de ecuaciones diferenciales lineales ordinarias con coeficientes constantes, que en un caso bastante general se pueden reducir a una ecuación diferencial ... Enciclopedia de tecnología Ecuación algebraica de la forma El determinante en esta fórmula se obtiene del determinante de la matriz restando el valor x de los elementos diagonales; es un polinomio en x y se llama polinomio característico ... Diccionario enciclopédico grande Ecuación característica- - [V.A. Semenov. Diccionario inglés ruso de relés de protección] Temas Protección de relés EN ecuación característica ... Guía del traductor técnico Ecuación algebraica de la forma. El determinante en esta fórmula se obtiene del determinante de la matriz x de los elementos diagonales; es un polinomio en x y se llama polinomio característico. * * * CARACTERÍSTICA ... ... diccionario enciclopédico Ecuación característica- būdingoji lygtis statusas T sritis automatika atitikmenys: angl. Ecuación característica; ecuación de rendimiento vok. charakteristische Gleichung, f; Stammgleichung, f rus. ecuación característica, n pranc. équation caractéristique, f… Automatikos terminų žodynas Ecuación característica- būdingoji lygtis statusas T sritis fizika atitikmenys: angl. Ecuación característica; ecuación de rendimiento vok. charakteristische Gleichung, f rus. ecuación característica, n pranc. équation caractéristique, f ... Fizikos terminų žodynas Ecuación característica Enciclopedia "Aviación" Ecuación característica- Ecuación característica. En muchos casos, los procesos físicos que ocurren en sistemas se describen mediante un sistema de ecuaciones diferenciales lineales ordinarias con coeficientes constantes, que en un caso bastante general se pueden reducir ... Enciclopedia "Aviación" La ecuación milenaria, ver art. El polinomio característico ... Enciclopedia de las matemáticas Un polinomio característico es un polinomio que determina los valores propios de una matriz. Otro significado: El polinomio característico de un recurrente lineal es un polinomio. Contenido 1 Definición ... Wikipedia La ecuación característica se elabora para el circuito después de la conmutación. Se puede obtener de las siguientes formas: De acuerdo con el primer método de la lección anterior, se obtuvo una ecuación diferencial para el voltaje a través del capacitor para un circuito serial R-L-C, sobre cuya base se escribe la ecuación característica. Cabe señalar que, dado que el circuito lineal está cubierto por un único proceso transitorio, las raíces de la ecuación característica son comunes para todos los componentes libres de los voltajes y corrientes de las ramas del circuito, cuyos parámetros se incluyen en la ecuación característica. . Por tanto, según el primer método de elaboración de la ecuación característica, se puede seleccionar cualquier variable con respecto a la que se escribe. Consideremos la aplicación del segundo y tercer método de elaboración de la ecuación característica utilizando el ejemplo del circuito de la Fig. 1. La elaboración de la ecuación característica utilizando el método de impedancia de entrada es la siguiente: se registra la resistencia de entrada del circuito de CA; jw se reemplaza por el operador p; la expresión resultante se pone a cero. La ecuacion coincide con la característica. Se debe enfatizar que la impedancia de entrada se puede escribir en relación con el punto de ruptura de cualquier rama del circuito. En este caso, la red activa de dos terminales se reemplaza por una pasiva, por analogía con el método de un generador equivalente. Este método de elaboración de la ecuación característica supone la ausencia de ramas acopladas magnéticamente en el circuito; en su caso, es necesario realizar su desamarre preliminar. Para la cadena de la fig. 1 con respecto a los terminales fuente Reemplazando jw con py igualando la expresión resultante a cero, escribimos Al elaborar una ecuación característica basada en la expresión del determinante principal, el número de ecuaciones algebraicas sobre cuya base se escribe es igual al número de componentes libres desconocidos de las corrientes. La algebraización del sistema original de ecuaciones integro-diferenciales, compilado, por ejemplo, sobre la base de las leyes de Kirchhoff o por el método de las corrientes de bucle, se lleva a cabo reemplazando los símbolos de diferenciación e integración, respectivamente, con multiplicación y división por el operador p. La ecuación característica se obtiene equiparando el determinante registrado a cero. Dado que la expresión del determinante principal no depende de los lados derechos del sistema de ecuaciones no homogéneas, puede elaborarse sobre la base de un sistema de ecuaciones escrito para corrientes totales. Para la cadena de la fig. 1 el sistema algebraizado de ecuaciones basado en el método de corriente de bucle tiene la forma De ahí la expresión del determinante principal de este sistema Igualando D a cero, obtenemos un resultado similar a (1). Método general para calcular procesos transitorios por el método clásico. En general, el método para calcular procesos transitorios por el método clásico incluye las siguientes etapas: Ejemplos de cálculo de procesos transitorios por el método clásico. 1. Procesos transitorios en el circuito R-L cuando está conectado a una fuente de voltaje Tales procesos tienen lugar, por ejemplo, cuando se conectan electroimanes, transformadores, motores eléctricos, etc. a una fuente de energía. Considere dos casos: De acuerdo con el método considerado para la corriente en el circuito en la Fig. 2 se pueden escribir Ecuación característica donde es la constante de tiempo Por lo tanto, Sustituyendo (4) y (5) en la relación (3), escribimos Según la primera ley de conmutación. Luego Por lo tanto, la corriente en el circuito en el proceso transitorio se describe mediante la ecuación y el voltaje a través del inductor, por la expresión La forma cualitativa de las curvas y correspondiente a las soluciones obtenidas se muestra en la Fig. 3. Para el segundo tipo de fuente, el componente forzado se calcula utilizando el método simbólico: La expresión del componente libre no depende del tipo de fuente de voltaje. Por eso, Desde entonces Por lo tanto, finalmente obtenemos El análisis de la expresión obtenida (6) muestra: Si es de magnitud significativa, entonces el componente libre no disminuye significativamente durante medio período. En este caso, el valor máximo de la corriente transitoria puede exceder significativamente la amplitud de la corriente de estado estable. Como se ve en la Fig. 4 donde Por lo tanto, para un circuito lineal, el valor máximo de la corriente transitoria no puede exceder la amplitud duplicada de la corriente forzada:. De manera similar para un circuito lineal con un capacitor: si en el momento de conmutar el voltaje forzado es igual a su valor de amplitud y la constante de tiempo del circuito es lo suficientemente grande, luego de aproximadamente la mitad del período, el voltaje en el capacitor alcanza su valor máximo , que no puede exceder la amplitud duplicada de la tensión forzada: 2. Transitorios cuando el inductor está desconectado de la fuente de alimentación Cuando se abre la llave en el circuito de la Fig. 5 componente forzada de la corriente a través del inductor. Ecuación característica dónde Según la primera ley de conmutación Por tanto, la expresión de la corriente transitoria y voltaje a través del inductor El análisis (7) muestra que cuando se abren circuitos que contienen elementos inductivos, pueden ocurrir grandes sobretensiones que, sin tomar medidas especiales, pueden dañar el equipo. De hecho, para 3. Carga y descarga de condensadores Cuando la llave se mueve a la posición 1 (ver Fig.6), comienza el proceso de carga del capacitor: Componente forzado del voltaje a través del capacitor. De la ecuación característica la raíz está determinada El modo libre del circuito no depende de las fuentes de energía, está determinado solo por la estructura del circuito y los parámetros de sus elementos. De esto se deduce que las raíces de la ecuación característica p1, p2,…, pn serán las mismas para todas las funciones variables (corrientes y tensiones). La ecuación característica se puede construir utilizando varios métodos. El primer método es clásico, cuando la ecuación característica se elabora estrictamente de acuerdo con la diferencial según el esquema clásico. Al calcular los transitorios en un circuito complejo, se elabora un sistema de ecuaciones diferenciales "m" de acuerdo con las leyes de Kirchhoff para el diagrama del circuito después de la conmutación. Dado que las raíces de la ecuación característica son comunes para todas las variables, la solución del sistema de ecuaciones diferenciales se realiza con respecto a cualquier variable (por elección). Como resultado de la solución, se obtiene una ecuación diferencial no homogénea con una variable. La ecuación característica se compila de acuerdo con el diferencial obtenido y se determinan sus raíces. Ejemplo. Elabore la ecuación característica y determine sus raíces para las variables en el circuito de la Fig. 59,1. Los parámetros de los elementos se establecen de forma general. Sistema de ecuaciones diferenciales según las leyes de Kirchhoff: Resolvamos el sistema de ecuaciones con respecto a la variable i3, como resultado obtenemos una ecuación diferencial no homogénea: La segunda forma de componer la ecuación característica es igualar a cero el principal determinante del sistema de ecuaciones de Kirchhoff para los componentes libres de las variables. Deje que el componente libre de una corriente arbitraria tenga la forma icv = Аkept, entonces: El sistema de ecuaciones para las componentes libres se obtiene a partir del sistema de ecuaciones diferenciales de Kirchhoff reemplazando las derivadas de las variables por el factor py las integrales por 1 / p. Para el ejemplo en consideración, el sistema de ecuaciones para los componentes libres tiene la forma: Ecuación característica y su raíz: El tercer método de elaboración de la ecuación característica (ingeniería) es igualar a cero la resistencia del operador de entrada del circuito con respecto a cualquiera de sus ramas. La resistencia del operador de un elemento se obtiene a partir de su resistencia compleja simplemente reemplazando el factor jω con p, por lo tanto Para el ejemplo en cuestión: El tercer método es el más simple y económico, por lo que se usa con mayor frecuencia para calcular transitorios en circuitos eléctricos. Las raíces de la ecuación característica caracterizan un proceso transitorio libre en un circuito sin fuentes de energía. Tal proceso avanza con pérdidas de energía y, por lo tanto, se extingue con el tiempo. De esto se deduce que las raíces de la ecuación característica deben ser negativas o tener una parte real negativa. En el caso general, el orden de la ecuación diferencial, que describe el proceso transitorio en el circuito, y, por lo tanto, el grado de la ecuación característica y el número de sus raíces son iguales al número de condiciones iniciales independientes, o el número de unidades de almacenamiento de energía independientes (bobinas L y condensadores C). Si el diagrama del circuito contiene condensadores conectados en paralelo C1, C2, ... o bobinas conectadas en serie L1, L2, ..., entonces, al calcular los procesos transitorios, deben reemplazarse con un elemento equivalente SE = C1 + C2 + ... o LE = L1 + L2 + ... Así, la visión general de la solución para cualquier variable en el cálculo del proceso transitorio se puede compilar solo a partir del análisis del diagrama del circuito, sin trazar y resolver un sistema de ecuaciones diferenciales. Para el ejemplo anterior.
se presenta en forma de sumatoria de las decisiones generales y privadas.
Vea qué es la "Ecuación característica" en otros diccionarios:
Libros
.
.
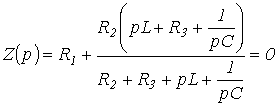
(1)
. .
(5)
.
,
,
.
,
. .
(6)
, la corriente máxima tiene lugar en aproximadamente. En el límite en.
.
,
y 
.
.
.
(7)
el módulo de voltaje en la bobina del inductor en el momento de la conmutación será muchas veces mayor que el voltaje de la fuente :. En ausencia de una resistencia de amortiguación R, el voltaje especificado se aplica a los contactos abiertos de la llave, como resultado de lo cual surge un arco entre ellos.
.
... De ahí la constante de tiempo.
