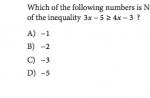Indeks antypatii php podstawowa matematyka. Rozwiązywanie problemu komiwojażera

Wykłady z matematyki elementarnej (1898) jest najwcześniejszym angielskim tłumaczeniem publikacji Josepha Louisa Lagrange'a z 1795 roku, Leçons élémentaires sur les mathematiques, zawierający cykl wykładów wygłoszonych w tym samym roku w Ecole Normale. Dzieło zostało przetłumaczone i zredagowane przez Thomasa J. McCormacka, a drugie wydanie, z którego zaczerpnięto poniższe cytaty, ukazało się w 1901 roku.

Zawartość

cytaty [edytować]

Wykład III. O algebrze, szczególnie rozwiązywaniu równań trzeciego i czwartego stopnia[edytować]

• Algebra jest nauką prawie w całości dzięki współczesnym... mamy bowiem jeden traktat od Greków, traktat Diofanta... jedyny, który zawdzięczamy starożytnym w tej dziedzinie matematyki. (...) Mówię tylko o Grekach, gdyż Rzymianie nic nie zostawili w nauce i, jak się wydaje, nic nie zrobili.

• Jego praca zawiera pierwsze elementy tej nauki. Do wyrażenia nieznanej ilości użył greckiej litery, która odpowiada naszemu NS i który został zastąpiony w tłumaczeniach przez n... Do wyrażania znanych wielkości używał wyłącznie liczb, ponieważ od dawna przeznaczeniem algebry było ograniczenie się wyłącznie do rozwiązywania problemów numerycznych.

• [H] e wykorzystuje zarówno znane, jak i nieznane wielkości. I tutaj sprowadza się właściwie do istoty algebry, która polega na wykorzystaniu nieznanych wielkości, obliczaniu nimi, tak jak robimy to ze znanymi wielkościami, i formułowaniu z nich jednego lub kilku równań, z których można wyznaczyć wartość nieznanych wielkości.

• Chociaż dzieło Diofantusa zawiera prawie wyłącznie problemy nieokreślone, których rozwiązania szuka w liczbach wymiernych — problemy, które zostały nazwane po nim — problemy diofantyczne, — niemniej jednak w jego pracy znajdujemy rozwiązanie szeregu określonych problemów pierwszego stopnia, a nawet takich, które obejmują kilka nieznanych wielkości. W tym drugim przypadku jednak autor niezmiennie ucieka się do… zredukowania problemu do jednej nieznanej wielkości, co nie jest trudne.

• Daje również rozwiązanie: równania drugiego stopnia, ale uważa, aby je ułożyć tak, aby nigdy nie przybrały odpowiedniej formy zawierającej kwadrat i pierwszą potęgę nieznanej wielkości. ...zawsze dochodzi do równania, w którym wystarczy wydobyć pierwiastek kwadratowy, aby znaleźć rozwiązanie ...

• Diophantus… nie wykracza poza równania drugiego stopnia i nie wiemy, czy on lub którykolwiek z jego następców… kiedykolwiek pchnął… poza ten punkt.

• Diophantus nie był znany w Europie aż do końca XVI wieku, pierwszy przekład był nędznym tłumaczeniem Xylandera wykonanym w 1575 roku. Bachet de Méziriac... jak na swoje czasy całkiem dobry matematyk, później opublikował (1621) nowe tłumaczenie ... z obszernymi komentarzami, teraz zbędnymi. Tłumaczenie Bacheta zostało później przedrukowane z obserwacjami i notatkami Fermata.

• Przed odkryciem i publikacją Diophantusa ... algebra już trafiła do Europy. Pod koniec XV wieku ukazało się w Wenecji dzieło... Lucasa Paciolusa o arytmetyce i geometrii, w którym podano elementarne zasady algebry.

• [T] e Europejczycy, otrzymawszy algebrę od Arabów, byli w jej posiadaniu na sto lat przed poznaniem dzieła Diofanta. Nie zrobili jednak żadnego postępu poza równaniami pierwszego i drugiego stopnia.

• W pracy Paciolusa... nie podano ogólnego rozwiązania równań drugiego stopnia.... Znajdujemy w tym dziele po prostu reguły, wyrażone w złych łacińskich wersetach, dotyczące rozwiązywania każdego konkretnego przypadku według różnych kombinacji znaków wyrazów równania, a nawet te reguły stosują się tylko do przypadku, gdy pierwiastki są rzeczywiste i dodatnie. Negatywne korzenie nadal uważano za bezsensowne i zbędne.

• To właśnie geometria naprawdę sugerowała nam użycie wielkości ujemnych, a tutaj zawiera jedną z największych zalet, jakie wynikły z zastosowania algebry do geometrii, krok, który zawdzięczamy Kartezjuszowi.

• W kolejnym okresie badano rozwiązanie równań trzeciego stopnia i odkrycia dla konkretnego przypadku dokonał ostatecznie... Scipio Ferreus (1515). ... Tartaglia i Cardan następnie udoskonalili rozwiązanie Ferreusa i uogólnili je dla wszystkich równań trzeciego stopnia.

• W tym okresie Włochy, które były kolebką algebry w Europie, były nadal prawie jedynym kultywatorem nauki i dopiero w połowie XVI wieku we Francji, Niemczech i Niemczech zaczęły pojawiać się traktaty o algebrze. inne kraje.

• Prace Peletier i Buteo były pierwszymi, które Francja stworzyła w tej nauce ...

• Tartaglia przedstawił swoje rozwiązanie kiepskimi włoskimi wierszami w dziele omawiającym różnorodne kwestie i wynalazki wydrukowanym w 1546 r., dziele, które cieszy się wyróżnieniem jako jedno z pierwszych, które traktuje o nowoczesnych fortyfikacjach przez bastiony.

• Cardan opublikował swój traktat Ars magna, lub Algebra... Cardan jako pierwszy zauważył, że równania mają kilka pierwiastków i rozróżnił je na dodatnie i ujemne. Ale jest szczególnie znany z tego, że jako pierwszy zauważył tzw nieredukowalny przypadek w której ekspresja prawdziwych korzeni pojawia się w wyimaginowanej formie. Cardan przekonał się na podstawie kilku szczególnych przypadków, w których równanie miało racjonalne dzielniki, że forma urojona nie uniemożliwia pierwiastkom posiadania prawdziwej wartości. Pozostało jednak do udowodnienia, że ​​nie tylko korzenie są rzeczywiste w przypadku nieredukowalnym, ale że niemożliwe jest, aby wszystkie trzy razem były rzeczywiste, z wyjątkiem tego przypadku. Dowód ten dostarczył później Vieta, a zwłaszcza Albert Girard, z rozważań dotyczących trisekcji kąta.

• [Ten nieredukowalny przypadek równań trzeciego stopnia... przedstawia nową formę wyrażeń algebraicznych, które znalazły szerokie zastosowanie w analizie ... stale podnosi się do nieopłacalnych badań w celu zredukowania formy urojonej do postaci rzeczywistej i ... w ten sposób przedstawia problem w algebrze które można postawić na tej samej podstawie ze słynnymi problemami powielania sześcianu i kwadratury koła w geometrii.

• Matematycy omawianego okresu zwykli przedstawiać sobie nawzajem problemy do rozwiązania. Były to... publiczne wyzwania i służyły podnieceniu i podtrzymaniu tej fermentacji, która jest niezbędna w dążeniu do nauki. Wyzwania… były kontynuowane aż do początku osiemnastowiecznej Europy i tak naprawdę nie ustały aż do powstania akademii, które spełniły ten sam cel… częściowo przez zjednoczenie wiedzy ich różnych członków, częściowo przez współżycie, które utrzymywali ... i ... przez publikację swoich wspomnień, które służyły rozpowszechnianiu nowych odkryć i obserwacji ...

• ten Algebra Bombelli zawiera nie tylko odkrycie Ferrari, ale także wiele innych ważnych uwag dotyczących równań drugiego i trzeciego stopnia, a zwłaszcza teorii pierwiastków, za pomocą których autorowi udało się w kilku przypadkach wydobyć wyimaginowane pierwiastki sześcienne z dwóch dwumianów formuły trzeciego stopnia w przypadku nieredukowalnym, a więc znalezienie doskonale rzeczywistego wyniku... możliwie najbardziej bezpośredniego dowodu na prawdziwość tego rodzaju wyrażeń.

• Szybko udało się rozwiązać równania III i IV stopnia. Ale kolejne wysiłki matematyków przez ponad dwa stulecia nie zdołały przezwyciężyć trudności równania piątego stopnia.

• Jednak te wysiłki nie poszły na marne. Dały one początek wielu pięknym twierdzeniom... o tworzeniu równań, o charakterze i znakach pierwiastków, o przekształceniu danego równania w inne, których pierwiastki mogą być formowane z przyjemnością z pierwiastków dane równanie i wreszcie do pięknych rozważań dotyczących metafizyki rozwiązywania równań, z których wynikła najbardziej bezpośrednia metoda dochodzenia do ich rozwiązania, o ile to możliwe.

• Vieta i Descartes… Harriot… i Hudde… byli pierwszymi po Włochach… którzy udoskonalili teorię równań, a od ich czasów prawie nie ma wybitnego matematyka, który by się nie zastosował…

Wykład V. O wykorzystaniu krzywych w rozwiązywaniu problemów[edytować]

• Dopóki algebra i geometria podróżowały oddzielnymi ścieżkami, ich postęp był powolny, a ich zastosowania ograniczone. Ale kiedy te dwie nauki połączyły się, czerpały od siebie świeżą witalność i odtąd maszerowały w szybkim tempie ku doskonałości. To Kartezjuszowi zawdzięczamy zastosowanie algebry do geometrii — zastosowania, które dostarczyło klucza do największych odkryć we wszystkich gałęziach matematyki.

• Metoda ... znajdowania i przedstawiania różnych ogólnych własności równań poprzez uwzględnienie krzywych, które je reprezentują, jest rodzajem zastosowania geometrii do algebry ... [T] jego metoda ma rozszerzone zastosowania i jest zdolna do łatwego rozwiązywania problemów którego bezpośrednie rozwiązanie byłoby niezwykle trudne, a nawet niemożliwe… [T] jego temat… zwykle nie znajduje się w elementarnych pracach z algebry.

• [A] n równanie dowolnego stopnia można rozwiązać za pomocą krzywej, której odcięte reprezentują nieznaną wielkość równania, a rzędne wartości, które przyjmuje lewy członek dla każdej wartości nieznanej wielkości . ... [T] jego metoda może być stosowana ogólnie do wszystkich równań, niezależnie od ich formy, i ... wymaga jedynie ich rozwinięcia i uporządkowania zgodnie z różnymi potęgami nieznanej wielkości.
[edytować]
• Wykłady z matematyki elementarnej 2. wyd. (1901) @Książki Google

Instrukcja. Aby uzyskać rozwiązanie problemu transportowego online, wybierz wymiar matrycy taryfowej (liczba dostawców i ilość sklepów).

W tym kalkulatorze używane są również następujące elementy:
Graficzna metoda rozwiązywania LPP
Metoda simplex do rozwiązywania LPP
Rozwiązanie do gry w macierz
Korzystając z usługi online możesz określić cenę gry macierzowej (dolne i górne granice), sprawdzić obecność punktu siodłowego, znaleźć rozwiązanie strategii mieszanej za pomocą metod: minimax, simplex, graficzna (geometryczna) metoda, metoda Browna.

Ekstremum funkcji dwóch zmiennych
Problemy z programowaniem dynamicznym

Pierwszy etap w rozwiązaniu problemu transportowego jest definicją jego typu (otwarta lub zamknięta lub w inny sposób zrównoważona lub niezrównoważona). Metody przybliżone ( metody znajdowania planu odniesienia) pozwalać na drugi krok decyzji w niewielkiej liczbie kroków, aby uzyskać możliwe do zrealizowania, ale nie zawsze optymalne rozwiązanie problemu. Ta grupa metod obejmuje metody:

• skreślenia (metoda podwójnej preferencji);
• narożnik północno-zachodni;
• element minimalny;
• Przybliżenie Vogla.

Podstawowe rozwiązanie problemu transportowego

Podstawowe rozwiązanie problemu transportowego nazywa się dowolnym rozwiązaniem dopuszczalnym, dla którego wektory warunków odpowiadające współrzędnym dodatnim są liniowo niezależne. Aby sprawdzić liniową niezależność wektorów warunków odpowiadających współrzędnym rozwiązania dopuszczalnego, stosuje się cykle.
Cykl nazywana jest sekwencją komórek w tabeli problemu transportu, w której dwie i tylko sąsiednie komórki znajdują się w tym samym wierszu lub kolumnie, a pierwsza i ostatnia komórka również znajdują się w tym samym wierszu lub kolumnie. Układ wektorów warunków problemu transportu jest liniowo niezależny wtedy i tylko wtedy, gdy z odpowiednich komórek tabeli nie można utworzyć jednego cyklu. Dlatego możliwe jest rozwiązanie problemu transportowego, i = 1,2, ..., m; j = 1,2, ..., n jest decydujące tylko wtedy, gdy z komórek tabeli przez niego zajmowanej nie można utworzyć żadnego cyklu.

Przybliżone metody rozwiązywania problemu transportowego.
Metoda skreślenia (metoda podwójnej preferencji)... Jeśli w wierszu lub kolumnie tabeli jest jedna zajęta komórka, to nie może wejść w żaden cykl, ponieważ cykl ma dwie i tylko dwie komórki w każdej kolumnie. Dlatego możesz wykreślić wszystkie wiersze tabeli zawierające jedną zajętą ​​komórkę, następnie wykreślić wszystkie kolumny zawierające jedną zajętą ​​komórkę, a następnie powrócić do wierszy i kontynuować usuwanie wierszy i kolumn. Jeżeli w wyniku usunięcia usuwane są wszystkie wiersze i kolumny, oznacza to, że części tworzącej cykl nie można wybrać z zajętych komórek tabeli, a układ odpowiadających im wektorów warunków jest liniowo niezależny, a rozwiązaniem jest wsparcie. Jeżeli po delecjach niektóre komórki pozostaną, to komórki te tworzą cykl, układ odpowiednich wektorów warunków jest liniowo zależny, a rozwiązanie nie jest podtrzymywane.
Metoda narożnika północno-zachodniego polega na sekwencyjnym wyliczaniu wierszy i kolumn tabeli transportów, zaczynając od lewej kolumny i górnego wiersza oraz wypisywanie maksymalnych możliwych wysyłek w odpowiednich komórkach tabeli tak, aby możliwości dostawcy lub wymagania konsumenta podane w zadaniu nie są przekroczone. W tej metodzie nie zwraca się uwagi na ceny dostaw, ponieważ zakłada się dalszą optymalizację wysyłek.
Metoda elementów minimalnych... Wyróżnia się prostotą, metoda ta jest jeszcze bardziej efektywna niż np. metoda narożnika północno-zachodniego. Ponadto metoda minimum elementów jest przejrzysta i logiczna. Jego istotą jest to, że najpierw w tabeli transportowej wpisywane są komórki z najniższymi taryfami, a następnie komórki z taryfami wysokimi. Oznacza to, że wybieramy transport z minimalnym kosztem dostarczenia ładunku. To oczywiste i logiczne posunięcie. To prawda, że ​​nie zawsze prowadzi to do optymalnego planu.
Metoda aproksymacji Vogla... Dzięki metodzie aproksymacji Vogla, w każdej iteracji we wszystkich kolumnach i we wszystkich wierszach znajduje się różnica między dwiema minimalnymi taryfami w nich zapisanymi. Różnice te są zapisywane w specjalnie wyznaczonej linii i kolumnie w tabeli stanów problemowych. Wśród tych różnic wybiera się minimum. W wierszu (lub w kolumnie), któremu odpowiada ta różnica, określana jest taryfa minimalna. Komórka, w której jest zapisany, jest wypełniana w tej iteracji.

Przykład 1. Macierz taryfowa (tu liczba dostawców to 4, liczba sklepów to 6):

	1	2	3	4	5	6	Dyby
1	3	20	8	13	4	100	80
2	4	4	18	14	3	0	60
3	10	4	18	8	6	0	30
4	7	19	17	10	1	100	60
Wymagania	10	30	40	50	70	30

Rozwiązanie. Wstępny etap rozwiązanie problemu transportowego sprowadza się do określenia jego rodzaju, czy jest otwarty czy zamknięty. Sprawdźmy warunek konieczny i wystarczający dla rozwiązania problemu.
∑a = 80 + 60 + 30 + 60 = 230
∑b = 10 + 30 + 40 + 50 + 70 + 30 = 230
Warunek równowagi jest spełniony. Zapasy odpowiadają potrzebom. Zatem model problemu transportowego jest zamknięty. Gdyby model okazał się otwarty, konieczne byłoby wprowadzenie dodatkowych dostawców lub odbiorców.
Na drugi etap wyszukiwanie planu referencyjnego odbywa się za pomocą metod podanych powyżej (najczęściej stosowana jest metoda najmniejszych kosztów).
Aby zademonstrować algorytm, przedstawiamy tylko kilka iteracji.
Iteracja nr 1. Minimalny element matrycy to zero. Dla tego elementu zapasy to 60, wymagania to 30. Wybieramy z nich minimalną liczbę 30 i odejmujemy ją (patrz tabela). W tym przypadku wykreślamy szóstą kolumnę z tabeli (jej potrzeby są równe 0).

3	20	8	13	4	x	80
4	4	18	14	3	0	60 - 30 = 30
10	4	18	8	6	x	30
7	19	17	0	1	x	60
10	30	40	50	70	30 - 30 = 0	0

Numer iteracji 2. Znowu szukam minimum (0). Z pary (60; 50) wybierz minimalną liczbę 50. Skreśl piątą kolumnę.

3	20	8	x	4	x	80
4	4	18	x	3	0	30
10	4	18	x	6	x	30
7	19	17	0	1	x	60 - 50 = 10
10	30	40	50 - 50 = 0	70	0	0

Numer iteracji 3. Kontynuujemy proces aż do wybrania wszystkich potrzeb i stanów magazynowych.
Numer iteracji Wymagany element to 8. Dla tego elementu zapasy są równe potrzebom (40).

3	x	8	x	4	x	40 - 40 = 0
x	x	x	x	3	0	0
x	4	x	x	x	x	0
x	x	x	0	1	x	0
0	0	40 - 40 = 0	0	0	0	0

	1	2	3	4	5	6	Dyby
1	3	20	8	13	4	100	80
2	4	4	18	14	3	0	60
3	10	4	18	8	6	0	30
4	7	19	17	0	1	100	60
Wymagania	10	30	40	50	70	30

Policzmy ilość zajętych komórek w tabeli, jest ich 8, a powinno być m + n - 1 = 9. W związku z tym plan wsparcia jest zdegenerowany. Budujemy nowy plan. Czasami konieczne jest zbudowanie kilku planów referencyjnych przed znalezieniem niezdegenerowanego.

	1	2	3	4	5	6	Dyby
1	3	20	8	13	4	100	80
2	4	4	18	14	3	0	60
3	10	4	18	8	6	0	30
4	7	19	17	0	1	100	60
Wymagania	10	30	40	50	70	30

W rezultacie uzyskuje się pierwszy plan odniesienia, który jest ważny, ponieważ liczba zajętych komórek w tabeli wynosi 9 i odpowiada formule m + n - 1 = 6 + 4 - 1 = 9, tj. linia bazowa to niezdegenerowany.
Trzeci etap jest udoskonalenie znalezionego planu referencyjnego. Tutaj używana jest potencjalna metoda lub metoda dystrybucji. Na tym etapie poprawność rozwiązania można kontrolować za pomocą funkcji kosztu F(x). Jeśli maleje (z zastrzeżeniem minimalizacji kosztów), to przebieg rozwiązania jest prawidłowy.

Przykład nr 2. Korzystając z metody taryfy minimalnej, złóż wstępny plan rozwiązania problemu transportowego. Sprawdź optymalność za pomocą potencjalnej metody.

	30	50	70	10	30	10
40	2	4	6	1	1	2
80	3	4	5	9	9	6
60	4	3	2	7	8	7
20	5	1	3	5	7	9

Przykład nr 3. Cztery fabryki słodyczy mogą produkować trzy rodzaje słodyczy. W tabeli przedstawiono koszty wytworzenia jednego centa (centów) wyrobów cukierniczych przez każdą fabrykę, zdolności produkcyjne fabryk (centów miesięcznie) oraz dzienne zapotrzebowanie na wyroby cukiernicze (centy miesięcznie). Opracuj plan produkcji słodyczy, który zminimalizuje całkowite koszty produkcji.

Notatka... Tutaj można wstępnie przetransponować tabelę kosztów, ponieważ w przypadku klasycznego sformułowania problemu transportu najpierw następują zdolności produkcyjne (produkcja), a następnie konsumenci.

Przykład nr 4. Do budowy obiektów cegły dostarczane są z trzech (I, II, III) fabryk. Fabryki posiadają w magazynach odpowiednio 50, 100 i 50 tysięcy sztuk. cegły. Obiekty wymagają odpowiednio 50, 70, 40 i 40 tysięcy jednostek. cegły. Taryfy (jednostki pieniężne/tys. jednostek) przedstawione są w tabeli. Utwórz plan transportu, który zminimalizuje całkowite koszty wysyłki.

zostanie zamknięty, jeśli:
A) a = 40, b = 45
B) a = 45, b = 40
B) a = 11, b = 12
Warunek zamkniętego problemu transportowego: ∑a = ∑b
Znajdujemy, ∑a = 35 + 20 + b = 55 + b; b = 60 + a
Otrzymujemy: 55 + b = 60 + a
Równość będzie obserwowana tylko dla a = 40, b = 45

SAT Math Test obejmuje szereg metod matematycznych, z naciskiem na rozwiązywanie problemów, modele matematyczne i strategiczne wykorzystanie wiedzy matematycznej.

SAT Math Test: wszystko jest jak w prawdziwym świecie

Zamiast sprawdzać cię w każdym temacie matematyki, nowy SAT sprawdza twoją umiejętność korzystania z matematyki, na której będziesz polegać w większości przypadków i w wielu różnych sytuacjach. Pytania na teście z matematyki mają na celu odzwierciedlenie rozwiązania problemów i modeli, z którymi będziesz miał do czynienia

studia uniwersyteckie, studiujące bezpośrednio matematykę oraz nauki przyrodnicze i społeczne;
- codzienne czynności zawodowe;
- Twoje codzienne życie.

Na przykład, aby odpowiedzieć na niektóre pytania, będziesz musiał wykonać kilka kroków - ponieważ w prawdziwym świecie sytuacje, w których wystarczy jeden prosty krok, aby znaleźć rozwiązanie, są niezwykle rzadkie.

Format matematyki SAT

Test z matematyki SAT: podstawowe fakty

Część Matematyka SAT koncentruje się na trzech obszarach matematyki, które odgrywają wiodącą rolę w większości dyscyplin akademickich w szkolnictwie wyższym i karierze zawodowej:
- Serce algebry: Podstawy algebry, która koncentruje się na rozwiązywaniu równań i układów liniowych;
- Rozwiązywanie problemów i analiza danych: Rozwiązywanie problemów i analiza danych, które są niezbędne do ogólnej znajomości matematyki;
- Paszport do zaawansowanej matematyki: Fundamentals of Higher Mathematics, która zadaje pytania wymagające manipulacji złożonymi równaniami.
Test z matematyki opiera się również na dodatkowych tematach z matematyki, w tym geometrii i trygonometrii, które są najważniejsze dla studiów uniwersyteckich i kariery zawodowej.

Test z matematyki SAT: wideo

Podstawy algebry
Serce algebry

Ta sekcja matematyki SAT koncentruje się na algebrze i kluczowych pojęciach, które są najbardziej krytyczne dla sukcesu w college'u i karierze. Ocenia umiejętność analizowania, swobodnego rozwiązywania i konstruowania równań i nierówności liniowych. Studenci będą również musieli analizować i swobodnie rozwiązywać równania i układy równań kilkoma metodami.Aby w pełni docenić wiedzę z tego materiału, problemy będą się znacznie różnić pod względem formy i treści. Mogą być wystarczająco proste lub wymagać strategicznego myślenia i zrozumienia, na przykład interpretacji interakcji między wyrażeniami graficznymi i algebraicznymi, lub reprezentować rozwiązanie jako proces rozumowania. Zdający muszą wykazać się nie tylko znajomością metodologii rozwiązywania, ale także głębszym zrozumieniem pojęć leżących u podstaw równań i funkcji liniowych. Podstawy algebry SAT Matematyka jest oceniana w skali od 1 do 15.

W tej części znajdą się zadania, na które odpowiedź jest prezentowana metodą wielokrotnego wyboru lub samodzielnie obliczona przez ucznia. Korzystanie z kalkulatora jest czasami dozwolone, ale nie zawsze konieczne lub zalecane.

1. Skonstruuj, rozwiąż lub zinterpretuj wyrażenie liniowe lub równanie z jedną zmienną w kontekście określonych warunków. Wyrażenie lub równanie może mieć współczynniki wymierne, a uproszczenie wyrażenia lub rozwiązania równania może wymagać kilku kroków.

2. Konstruować, rozwiązywać lub interpretować nierówności liniowe za pomocą jednej zmiennej w kontekście określonych warunków. Nierówność może mieć racjonalne współczynniki i może wymagać kilku kroków w celu uproszczenia lub rozwiązania.

3. Skonstruuj funkcję liniową, która modeluje liniową zależność między dwiema wielkościami. Zdający musi opisać zależność liniową, która wyraża pewne warunki za pomocą równania z dwiema zmiennymi lub funkcji. Równanie lub funkcja będą miały wymierne współczynniki, a zbudowanie i uproszczenie równania lub funkcji może wymagać kilku kroków.

4. Konstruować, rozwiązywać i interpretować układy nierówności liniowych w dwóch zmiennych. Zdający przeanalizuje jeden lub więcej warunków, które istnieją między dwiema zmiennymi, konstruując, rozwiązując lub interpretując nierówność z dwiema zmiennymi lub system nierówności z dwiema zmiennymi, w ramach pewnych określonych warunków. Aby skonstruować nierówność lub system nierówności, można wykonać kilka kroków lub zdefiniować.

5. Konstruować, rozwiązywać i interpretować układ dwóch równań liniowych dla dwóch zmiennych. Zdający przeanalizuje jeden lub więcej warunków, które istnieją między dwiema zmiennymi, konstruując, rozwiązując lub analizując układ równań liniowych, w ramach pewnych określonych warunków. Równania będą miały racjonalne współczynniki i może być konieczne wykonanie kilku kroków w celu uproszczenia lub rozwiązania systemu.

6. Rozwiąż równania liniowe (lub nierówności) z jedną zmienną. Równanie (lub nierówność) będzie miało racjonalne współczynniki i może wymagać kilku kroków do rozwiązania. Równania mogą nie mieć rozwiązania, mieć jedno rozwiązanie lub mieć nieskończoną liczbę rozwiązań. Zdający może być również poproszony o określenie wartości lub współczynnika równania, które nie ma rozwiązania lub ma nieskończoną liczbę rozwiązań.

7. Rozwiąż układ dwóch równań liniowych w dwóch zmiennych. Równania będą miały współczynniki wymierne, a system może nie mieć żadnego rozwiązania, jednego rozwiązania lub nieskończonej liczby rozwiązań. Zdający może być również poproszony o określenie wartości lub współczynnika równania, w którym układ może nie mieć rozwiązania, mieć jedno rozwiązanie lub mieć nieskończoną liczbę rozwiązań.

8. Wyjaśnij związek między wyrażeniami algebraicznymi i graficznymi. Określ wykres opisany przez dane równanie liniowe lub równanie liniowe opisujące dany wykres, określ równanie linii podanej przez ustny opis jej wykresu, określ kluczowe cechy wykresu funkcji liniowej z jego równania, określ sposób zmiana w jego równaniu może wpłynąć na wykres.

Rozwiązywanie problemów i analiza danych
Rozwiązywanie problemów i analiza danych

Ta sekcja matematyki SAT odzwierciedla wyniki badań, które zidentyfikowały to, co jest ważne dla udanych studiów wyższych lub uniwersyteckich. Testy wymagają rozwiązywania problemów i analizy danych: umiejętności matematycznego opisu określonej sytuacji z uwzględnieniem elementów, poznania i wykorzystania różnych właściwości operacji matematycznych i liczb. Problemy z tej kategorii będą wymagały dużego doświadczenia w logicznym rozumowaniu.

Zdający będą musieli znać obliczanie średnich wartości wskaźników, ogólnych wzorców i odchyleń od ogólnego obrazu oraz rozkładów w zestawach.

Wszystkie rozwiązywanie problemów i analiza danych kwestionują zdolność osób testujących do wykorzystania ich rozumienia matematycznego i umiejętności do rozwiązywania problemów, z którymi mogą się zetknąć w prawdziwym świecie. Wiele z tych problemów pojawia się w kontekście akademickim i zawodowym i jest bardziej prawdopodobne, że jest związanych z nauką i socjologią.

Rozwiązywanie problemów i analiza danych to jeden z trzech podrozdziałów SAT Math, za którego rozwiązanie przyznaje się punkty od 1 do 15.

W tej sekcji będą zadania z odpowiedziami wielokrotnego wyboru lub samodzielnie obliczonymi przez zdającego. Korzystanie z kalkulatora jest tutaj zawsze dozwolone, ale nie zawsze konieczne lub zalecane.

W tej części SAT Math możesz natknąć się na następujące pytania:

1. Używaj kursów, kursów, proporcji i rysunków w skali do rozwiązywania problemów jedno- i wieloetapowych. Zdający będą używać proporcjonalnej relacji między dwiema zmiennymi, aby rozwiązać wieloetapowy problem w celu określenia przełożenia lub prędkości; Oblicz stosunek lub współczynnik, a następnie rozwiąż problem wieloetapowy, używając podanego współczynnika lub współczynnika, rozwiąż problem wieloetapowy.

2. Rozwiązuj jedno- i wieloetapowe problemy za pomocą procentów. Zdający rozwiąże problem wielopoziomowy, aby określić procent. Oblicz procent liczby, a następnie rozwiąż problem wielopoziomowy. Używając podanej wartości procentowej, rozwiąż problem wielopoziomowy.

3. Rozwiązuj jedno- i wieloetapowe problemy obliczeniowe. Zdający rozwiąże problem wielopoziomowy w celu ustalenia jednostki stawki; Oblicz jednostkę miary, a następnie rozwiąż problem wieloetapowy; Rozwiąż wielopoziomowe zadanie, aby zakończyć konwersję jednostek; Rozwiąż wielostopniowy problem z obliczaniem gęstości; Lub użyj koncepcji gęstości, aby rozwiązać wieloetapowy problem.

4. Używając diagramów rozrzutu, rozwiąż modele liniowe, kwadratowe lub wykładnicze, aby opisać, jak zmienne są powiązane. Mając wykres rozrzutu, wybierz równanie dla dopasowania linii lub krzywej; Zinterpretuj linię w kontekście sytuacji; Lub użyj linii lub krzywej, które najlepiej pasują do Twojej prognozy.

5. Korzystając z relacji między dwiema zmiennymi, zbadaj kluczowe funkcje wykresu. Zdający ustali powiązania między graficznym wyrażeniem danych a właściwościami wykresu, wybierając wykres, który reprezentuje opisane właściwości, lub używając wykresu, aby zdefiniować wartości lub zestawy wartości.

6. Porównaj wzrost liniowy ze wzrostem wykładniczym. Egzaminowany będzie musiał znaleźć dopasowanie między dwiema zmiennymi, aby określić, który typ modelu jest optymalny.

7, Używając tabel, oblicz dane dla różnych kategorii wielkości, względnych częstotliwości i prawdopodobieństw warunkowych. Badany wykorzystuje dane w różnych kategoriach do obliczenia częstości warunkowych, prawdopodobieństw warunkowych, powiązania zmiennych lub niezależności zdarzeń.

8. Wyciągnij wnioski dotyczące parametrów populacji na podstawie danych z próby. Kandydat ocenia parametr populacji na podstawie wyników losowej próby populacji. Statystyka próbki może zapewnić przedziały ufności i niepewności pomiaru, które uczeń musi zrozumieć i wykorzystać bez konieczności ich obliczania.

9. Używaj metod statystycznych do obliczania średnich i spreadów. Zdający obliczą średnią i / lub rozkład dla danego zestawu danych lub użyją statystyk do porównania dwóch oddzielnych zestawów danych.

10. Oceniaj raporty, wyciągaj wnioski, uzasadniaj wnioski i określaj adekwatność metod zbierania danych. Raporty mogą składać się z tabel, wykresów lub podsumowań tekstowych.

Podstawy matematyki wyższej
Paszport do zaawansowanej matematyki

Ta sekcja matematyki SAT zawiera tematy, które są szczególnie ważne dla uczniów do opanowania przed rozpoczęciem nauki matematyki wyższej. Kluczem jest zrozumienie struktury wyrażeń oraz umiejętność analizowania, manipulowania i upraszczania tych wyrażeń. Obejmuje również możliwość analizowania bardziej złożonych równań i funkcji.

Podobnie jak w dwóch poprzednich sekcjach matematyki SAT, zadania tutaj są oceniane od 1 do 15.

Ta sekcja będzie zawierała zadania wielokrotnego wyboru lub zadania obliczane samodzielnie.Używanie kalkulatora jest czasami dozwolone, ale nie zawsze jest konieczne lub zalecane.

W tej części SAT Math możesz natknąć się na następujące pytania:

1. Napisz funkcję lub równanie kwadratowe lub wykładnicze, które modelują te warunki. Równanie będzie miało racjonalne współczynniki i może wymagać kilku kroków w celu uproszczenia lub rozwiązania.

2. Określ najbardziej odpowiednią formę wyrażenia lub równania w celu zidentyfikowania konkretnego objawu w określonych warunkach.

3. Konstruować ekwiwalentne wyrażenia obejmujące wykładniki wymierne i pierwiastki, w tym uproszczenie lub przekształcenie w inną formę.

4. Konstruować równoważną formę wyrażenia algebraicznego.

5. Rozwiąż równanie kwadratowe ze współczynnikami wymiernymi. Równanie można przedstawić w wielu różnych formach.

6. Dodaj, odejmij i pomnóż wielomiany i uprość wynik. Wyrażenia będą miały współczynniki wymierne.

7. Rozwiąż równanie w jednej zmiennej, która zawiera pierwiastki lub zawiera zmienną w mianowniku ułamka. Równanie będzie miało racjonalne współczynniki.

8. Rozwiąż układ równań liniowych lub kwadratowych. Równania będą miały współczynniki wymierne.

9. Uprość proste wyrażenia wymierne. Zdający będą dodawać, odejmować, mnożyć lub dzielić dwa wyrażenia wymierne lub dzielić dwa wielomiany i upraszczać je. Wyrażenia będą miały współczynniki wymierne.

10. Interpretować fragmenty wyrażeń nieliniowych pod kątem ich warunków. Zdający muszą powiązać określone warunki z nieliniowym równaniem, które modeluje te warunki.

11. Rozumieć zależność między zerami a czynnikami w wielomianach i wykorzystywać tę wiedzę do tworzenia wykresów. Zdający będą używać właściwości wielomianów do rozwiązywania problemów z zerami, takich jak określanie, czy wyrażenie jest czynnikiem wielomianu na podstawie dostarczonych informacji.

12. Zrozum związek między dwiema zmiennymi poprzez ustalenie relacji między ich wyrażeniami algebraicznymi i graficznymi. Zdający musi umieć wybrać wykres, który odpowiada danemu równaniu nieliniowemu; interpretować grafy w kontekście rozwiązywania układów równań; wybierz równanie nieliniowe odpowiadające temu wykresowi; określić równanie krzywej, biorąc pod uwagę słowny opis wykresu; określić kluczowe cechy wykresu funkcji liniowej na podstawie jego równania; określić wpływ na wykres zmian w rządzącym równaniu.

Czego sprawdza sekcja matematyki w SAT Math

Ogólna znajomość dyscypliny

Test z matematyki to szansa na pokazanie, że:

Wykonuj zadania matematyczne elastycznie, dokładnie, wydajnie i przy użyciu strategii rozwiązania;
- Szybko rozwiązuj problemy, identyfikując i stosując najskuteczniejsze podejścia do rozwiązywania. Może to obejmować rozwiązywanie problemów poprzez:
zastępowanie, wyszukiwanie skrótów lub reorganizacja podanych przez Ciebie informacji;

Koncepcyjne rozumienie

Wykażesz się zrozumieniem pojęć matematycznych, operacji i relacji. Na przykład możesz zostać poproszony o ustalenie relacji między właściwościami równań liniowych, ich wykresami i warunkami, które wyrażają.

Stosowanie wiedzy na ten temat

Wiele zadań SAT Math pochodzi z rzeczywistych problemów i wymaga przeanalizowania tego problemu, zidentyfikowania podstawowych elementów potrzebnych do jego rozwiązania, matematycznego wyrażenia problemu i znalezienia rozwiązania.

Korzystanie z kalkulatora

Kalkulatory to podstawowe narzędzia do wykonywania obliczeń matematycznych. Aby z powodzeniem studiować na uniwersytecie, musisz wiedzieć, jak i kiedy z nich korzystać. W części testu Math Test-Calculator możesz skoncentrować się na rzeczywistym wyszukiwaniu i analizie rozwiązań, ponieważ Twój kalkulator pozwoli Ci zaoszczędzić czas.

Niemniej jednak kalkulator, jak każde narzędzie, jest tak samo inteligentny, jak ten, kto go używa. W teście z matematyki jest kilka pytań, w których najlepiej nie używać kalkulatora, nawet jeśli jest to dozwolone. W takich sytuacjach osoby testujące, które potrafią myśleć i rozumować, częściej udzielają odpowiedzi wcześniej niż osoby, które ślepo używają kalkulatora.

Część Test z matematyki — bez kalkulatora ułatwia ocenę ogólnej wiedzy na dany temat i zrozumienie niektórych pojęć matematycznych. Testuje również znajomość technik obliczeniowych i rozumienie pojęcia liczb.

Pytania z odpowiedziami do tabeli

Chociaż większość pytań testowych z matematyki to pytania wielokrotnego wyboru, 22 procent to pytania, na które odpowiedzi są wynikiem własnych obliczeń osoby zdającego — są to tzw. Zamiast wybierać poprawną odpowiedź z listy, musisz rozwiązać zadania i wpisać swoje odpowiedzi w kratkach wskazanych w arkuszu odpowiedzi.

Odpowiedzi tabelaryczne

Zaznacz nie więcej niż jeden okrąg w dowolnej kolumnie;
- Liczone będą tylko odpowiedzi wskazane przez wypełnienie kółka (nie otrzymasz punktów za wszystko wpisane w pola powyżej)
koła).
- Nie ma znaczenia, w której kolumnie zaczniesz wpisywać swoje odpowiedzi; ważne jest, aby odpowiedzi były zapisane w siatce, wtedy otrzymasz punkty;
- Siatka może zawierać tylko cztery miejsca po przecinku i może przyjmować tylko liczby dodatnie i zero.
- O ile w zadaniu nie określono inaczej, odpowiedzi można wprowadzać do siatki jako dziesiętne i ułamkowe;
- Ułamki takie jak 3/24 nie muszą być redukowane do wartości minimalnych;
- Wszystkie liczby mieszane muszą zostać przekonwertowane na ułamki niewłaściwe przed zapisaniem do siatki;
- Jeśli odpowiedź jest powtarzalną liczbą dziesiętną, uczniowie powinni ustawić najdokładniejsze wartości, które będą
rozważać.

Poniżej znajduje się przykładowa instrukcja, którą zdający zobaczą na egzaminie SAT z matematyki:

Lesia M. Ohnivchuk

Abstrakcyjny

Artykuł rozważa możliwość rozszerzenia funkcjonalności LMS Moodle przy tworzeniu kursów e-learningowych dla nauk matematycznych, w szczególności kursów e-learningowych "Matematyka elementarna" poprzez wykorzystanie technologii flash i apletów Java. W kursie „Matematyka elementarna” są przykłady użycia aplikacji flash i apletów Java.

Słowa kluczowe

LMS Moodle; kursy e-learningowe; technologia flash; Aplet Java, GeoGebra

Bibliografia

Brandão, L. O., „iGeom: darmowe oprogramowanie do dynamicznej geometrii w sieci”, Międzynarodowa Konferencja Nauki i Edukacji Matematycznej, Rio de Janeiro, Brazylia, 2002.

Brandão, L. O. i Eisnmann, A. L. K. „Praca w toku: iComb Project - widget matematyczny do nauczania i uczenia się kombinatoryki poprzez ćwiczenia” Proceedings of 39th ASEE / IEEE Frontiers in Education Conference, 2009, T4G_1–2

Kamiya, R. H i Brandão, L. O. „iVProg - system do programowania wprowadzającego poprzez Model Wizualny w Internecie. Obrady XX Simpósio Brasileiro de Informática na Educação, 2009 (w języku portugalskim).

Moodle.org: społecznościowe narzędzia typu open source do nauki [zasoby elektroniczne]. - Tryb dostępu: http://www.moodle.org.

MoodleDocs [Zasoby elektroniczne]. - Tryb dostępu: http://docs.moodle.org.

Interaktywne technologie nauki: teoria, praktyka, porady: księga metodyczna autorów: O. Pometun, L. Pirozhenko. - K.: APN; 2004 .-- 136 s.

Dmitrija Pupinina. Typ pytania: Flash [Zasób elektroniczny]. - Tryb dostępu: https://moodle.org/mod/data/view.php?d=13&rid=2493&filter=1 - 26.02.14.

Andreev A. V., Gerasimenko PS. Używanie Flash i SCORM do tworzenia końcowych zadań kontrolnych [Zasoby elektroniczne]. - Tryb dostępu: http://cdp.tti.sfedu.ru/index.php?option=com_content&task=view&id=1071&Itemid=363 –26.02.14.

GeoGebra. Materiały [Zasób elektroniczny]. - Tryb dostępu: http://tube.geogebra.org.

Hohenvator M. Wprowadzenie do GeoGebra / M. Hohenvator / os. T. S. Ryabowa. - 2012 .-- 153 s.

ODNIESIENIA (TŁUMACZONE I TRANSLITEROWANE)

Brandão, L. O. „iGeom: darmowe oprogramowanie do dynamicznej geometrii w sieci”, Międzynarodowa Konferencja Nauki i Edukacji Matematycznej, Rio de Janeiro, Brazylia, 2002 (w języku angielskim).

Brandão, L. O. i Eisnmann, A. L. K. „Praca w toku: iComb Project - widget matematyczny do nauczania i uczenia się kombinatoryki poprzez ćwiczenia” Proceedings of the 39th ASEE / IEEE Frontiers in Education Conference, 2009, T4G_1–2 (w języku angielskim).

Kamiya, R. H i Brandão, L. O. „iVProg - system do programowania wprowadzającego poprzez Model Wizualny w Internecie. Obrady XX Simpósio Brasileiro de Informática na Educação, 2009 (w języku angielskim) ..

Moodle.org: narzędzia do nauki oparte na społecznościach typu open source. - Dostępne na: http://www.moodle.org (w języku angielskim).

MoodleDocs. - Dostępne na: http://docs.moodle.org (w języku angielskim).

Pometun O. I., Pirozhenko L. V. Lekcja współczesna, Kijów, ASK Publ., 2004, 192 s. (w języku ukraińskim).

Dmitrija Pupinina. Typ pytania: Flash. - Dostępne pod adresem: https://moodle.org/mod/data/view.php?d=13&rid=2493&filter=1 - 26.02.14 (w języku angielskim).

Andreev A., Gerasimenko R. Wykorzystanie Flash i SCORM do tworzenia końcowej kontroli zadań. - Dostępne pod adresem: http://cdp.tti.sfedu.ru/index.php?option=com_content&task=view&id=1071&Itemid=363 - 26.02.14 (w języku rosyjskim).

GeoGebra Wiki. - Dostępne na: http://www.geogebra.org (w języku angielskim).

Hohenwarter M. Wprowadzenie w GeoGebra / M. Hohenwarter. - 2012 .-- 153 s. (po angielsku).

DOI: https://doi.org/10.33407/itlt.v48i4.1249

Copyright (c) 2015 Lesia M. Ohnivchuk