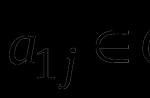بیضوی هایپربلوئیدها

بیضوی- سطحی در فضای سه بعدی که با تغییر شکل یک کره در امتداد سه محور عمود بر هم بدست می آید. معادله متعارف بیضی در مختصات دکارتی همزمان با محورهای تغییر شکل بیضی:

مقادیر a ، b ، c را نیم محور بیضی می نامند. بیضی نامیده می شود جسمی است که توسط سطح بیضی شکل محدود شده است. بیضی شکل یکی از اشکال احتمالی سطح دوم است.

در صورتی که یک جفت نیم محور دارای طول یکسان باشد ، می توان با چرخاندن بیضی به دور یکی از محورهای آن ، بیضی شکل به دست آورد. چنین بیضی شکل را بیضوی انقلاب یا کروی می نامند.

بیضی شکل با دقت بیشتری نسبت به کره ، سطح ایده آل شده زمین را منعکس می کند.

حجم بیضوی:.

سطح یک بیضوی انقلاب:

هایپربلوئید- این نوع سطح مرتبه دوم در فضای سه بعدی است ، که در مختصات دکارتی با معادله مشخص شده است- (هایپربلوئید یک ورقه) ، که در آن a و b نیم محورهای واقعی هستند و c یک نیم محور خیالی است. یا - (هایپربلوئید دو صفحه ای) ، که در آن a و b نیم محورهای فرضی هستند و c یک نیم محور واقعی است.

اگر a = b باشد ، چنین سطحی را هیپربلوئید انقلاب می نامند. یک هیپربلوئید یک صفحه ای از انقلاب را می توان با چرخاندن هایپربولا حول محور خیالی خود و یک هیپربلوئید دو صفحه ای حول محور واقعی آن به دست آورد. یک هایپربلوئید دو صفحه ای از انقلاب نیز محل نقاط P است ، مدول تفاوت بین فاصله هایی که از آن تا دو نقطه A و B مشخص است ثابت است: | AP - BP | = const در این حالت ، A و B کانون هایپربلوئید نامیده می شوند.

هایپربلوئید یک ورقه یک سطح دو خط است. اگر یک هذلولی از انقلاب است ، می توان آن را با چرخاندن یک خط مستقیم در اطراف خط مستقیم دیگری که با آن قطع می شود بدست آورد.

پارابولوئید- نوع سطح مرتبه دوم. یک پارابلوئید را می توان به عنوان یک سطح خارج از مرکز باز (یعنی بدون مرکز تقارن) سطح مرتبه دوم مشخص کرد.

معادلات متعارف یک پارابلوئید در مختصات دکارتی:

· اگر a و b علامت یکسانی داشته باشند ، پارابوئید بیضوی نامیده می شود.

· اگر a و b علامت مخالف داشته باشند ، در این صورت پارابلوئید هذلولی نامیده می شود.

· اگر یکی از ضرایب مساوی صفر باشد ، پارابلوئید استوانه سهموی نامیده می شود.

ü - پارابلوئید بیضوی ، که در آن a و b یک علامت هستند. سطح توسط خانواده ای از Parabolas های موازی با شاخه هایی به سمت بالا توصیف می شود که رأس آنها یک Parabola را توصیف می کند و شاخه ها نیز به سمت بالا اشاره می کنند. اگر a = b باشد ، پارابوئید بیضوی سطحی از چرخش است که از چرخش پارابولا حول محور عمودی که از راس این پارابولا عبور می کند تشکیل شده است.

ü - پارابولوئید هذلولی.

خاصیت اثبات شده مماس بر سهمی بسیار مهم است ، زیرا از آن نتیجه می گیرد که اشعه هایی که از کانون یک آینه سهموی مقعر منشعب می شوند ، یعنی آینه ای که سطح آن از چرخش فلکه حول محور خود بدست می آید ، توسط یک پرتو موازی ، یعنی محور آینه موازی (شکل) منعکس می شوند.

این ویژگی از آینه های سهمی در ساخت چراغهای جلو ، در چراغهای جلو هر خودرو و همچنین در تلسکوپهای آینه ای استفاده می شود. در این مورد ، در مورد دوم ، برعکس ، اشعه هایی که از بدن آسمانی می آیند ؛ تقریباً موازی ، آنها در نزدیکی کانون آینه تلسکوپ متمرکز شده اند و از آنجا که پرتوهای ناشی از نقاط مختلف نور بسیار غیر موازی هستند ، آنها در نزدیک نقطه کانونی در نقاط مختلف متمرکز شده اند ، به طوری که تصویری از نور به دست آمده در نزدیکی نقطه کانونی ، هر چه بیشتر ، فاصله کانونی Parabola بیشتر است. این تصویر قبلاً از طریق میکروسکوپ (چشمی تلسکوپ) مشاهده شده است. به طور دقیق ، فقط پرتوهای کاملاً موازی با محور آینه در یک نقطه (در کانون) جمع آوری می شوند ، در حالی که پرتوهای موازی ، که به زاویه ای به محور آینه می روند ، تقریباً در یک نقطه جمع می شوند ، و هرچه دورتر نقطه از فوکوس است ، تصویر تارتر است. این شرایط "میدان دید تلسکوپ" را محدود می کند.

اجازه دهید سطح داخلی آن - سطح آینه - این آینه سهمی با پرتویی از پرتوهای نور موازی با محور OU روشن شود. پس از بازتاب ، همه پرتوهای موازی با محور OY در یک نقطه از محور OY قطع می شوند (تمرکز F). طراحی تلسکوپ های سهمی بر اساس این ویژگی است. اشعه های ستارگان دور به صورت یک پرتو موازی به ما می رسند. با ساختن یک تلسکوپ سهمی و قرار دادن یک صفحه عکاسی در کانون آن ، ما این فرصت را پیدا می کنیم که سیگنال نوری را که از ستاره می آید تقویت کنیم.

همین اصل بر ایجاد یک آنتن سهمی است که به شما امکان می دهد سیگنال های رادیویی را تقویت کنید. اگر منبع نوری در کانون آینه سهمی قرار گیرد ، پس از بازتاب از سطح آینه ، اشعه های ناشی از این منبع پراکنده نمی شوند ، بلکه در یک پرتو باریک موازی با محور آینه جمع می شوند. . این واقعیت در ساخت پروژکتورها و فانوس ها ، پروژکتورهای مختلف ، که آینه های آنها به شکل پارابولوئید ساخته شده است ، کاربرد دارد.

ویژگی نوری آینه سهمی برای ایجاد تلسکوپ های آینه ای ، تاسیسات مختلف گرمایش خورشیدی و نورافکن ها استفاده می شود. با قرار دادن یک منبع نقطه ای قدرتمند نور در کانون یک آینه سهمی ، ما یک جریان متراکم از اشعه های منعکس شده موازی با محور آینه را بدست می آوریم.

وقتی یک سهمی حول محور خود می چرخد ​​، یک رقم به دست می آید که به آن پارابلوئید می گویند. اگر سطح داخلی پارابلوئید آینه کاری شود و پرتویی از پرتوهای موازی با محور تقارن سهمی به آن هدایت شود ، آنگاه اشعه های منعکس شده در یک نقطه جمع می شوند که به آن تمرکز می گویند. در عین حال ، اگر منبع نور در فوکوس قرار گیرد ، اشعه های منعکس شده از سطح آینه پارابلوئید موازی بوده و پراکنده نخواهند بود.

اولین ویژگی این است که می توان درجه حرارت بالا را در تمرکز پارابوئید بدست آورد. طبق افسانه ها ، این ویژگی توسط دانشمند یونان باستان ارشمیدس (287-212 قبل از میلاد) استفاده شده است. وی در حین دفاع از سیراکوز در جنگ علیه رومی ها ، سیستم آینه های سهمی را ساخت که به موجب آن می توان اشعه های منعکس شده خورشید را بر روی کشتی های رومیان متمرکز کرد. در نتیجه ، درجه حرارت در کانون آینه های سهمی به حدی بالا رفت که آتش بر کشتی ها رخ داد و آنها سوختند.

از ویژگی دوم ، به عنوان مثال ، در ساخت چراغهای جلو و چراغهای جلو اتومبیل استفاده می شود.

هذلولی

4. تعریف هایپربولا یک روش ساده برای ساختن آن در یک حرکت پیوسته به ما می دهد: دو رشته بگیرید که اختلاف طول آنها 2a است و یک سر این رشته ها را به نقاط F "و F وصل کنید. دو سر را با دست خود همراه کنید و با نوک مداد در امتداد رشته ها حرکت کنید ، مراقب باشید که نخ ها روی کاغذ فشرده ، محکم و لمس شوند ، از نوک نقاشی تا محل اتصال انتها شروع می شود ، نوک یک بخشی از یکی از شاخه های هایپربولا (هرچه بزرگتر باشد ، نخ ها طولانی تر گرفته می شوند) (شکل).

با تعویض نقش نقاط F "و F ، بخشی از شاخه دیگر را بدست می آوریم.

مثلا،در موضوع "منحنی های مرتبه 2" می توان مشکل زیر را در نظر گرفت:

یک وظیفه.دو ایستگاه راه آهن A و B در فاصله s کیلومتری یکدیگر واقع شده اند. محموله را می توان از ایستگاه A به هر نقطه M از طریق حمل و نقل مستقیم جاده ای (مسیر اول) ، یا از طریق راه آهن به ایستگاه B و از آنجا با اتومبیل (مسیر دوم) تحویل داد. تعرفه راه آهن (قیمت حمل و نقل 1 تن در هر کیلومتر) متر روبل ، تعرفه حمل و نقل جاده ای n روبل ، n> متر ، تعرفه بارگیری و تخلیه k روبل است. منطقه نفوذ ایستگاه راه آهن B را تعیین کنید ، یعنی منطقه ای که حمل محموله از ایستگاه A در مسیر ترکیبی ارزان تر است - از طریق راه آهن ، و سپس از طریق جاده ، یعنی. تعیین محل نقاطی که مسیر دوم برای آنها از اول مفیدتر است.

راه حل.ما AM = r ، BM = g را نشان می دهیم ، سپس هزینه تحویل (حمل و بارگیری و تخلیه) در طول مسیر AM برابر با nr + k و هزینه تحویل در طول مسیر ABM برابر با ms + 2k + ng است . سپس نقاط M ، که برای هر دو مقدار مساوی است ، معادله nr + k = ms + 2k + nг را برآورده می کند ، یا

ms + k = nr - ng

r - r = = const> 0 ،

بنابراین ، خطی که منطقه را محدود می کند یکی از شاخه های هایپربول | است r - r | = const برای همه نقاط هواپیما که در یک طرف با نقطه A از این ابرقرب قرار دارند ، مسیر اول مفیدتر است ، و برای نقاطی که در طرف دیگر قرار دارند ، مسیر دوم ، بنابراین ، شاخه هایپربولا منطقه نفوذ ایستگاه را ترسیم می کند. ب.

یک نوع از این وظیفه.

دو ایستگاه راه آهن A و B در فاصله 1 کیلومتری یکدیگر واقع شده اند. محموله را می توان از ایستگاه A از طریق ایستگاه A یا با حمل و نقل مستقیم جاده ای ، یا از طریق راه آهن به ایستگاه B و از آنجا با اتومبیل تحویل داد (شکل 49). در این مورد ، تعرفه راه آهن (قیمت حمل و نقل 1 تن در هر کیلومتر) متر روبل ، بارگیری - هزینه تخلیه k روبل (در هر تن) ، و تعرفه حمل و نقل جاده ای n روبل (n> متر) است. اجازه دهید منطقه به اصطلاح نفوذ ایستگاه راه آهن B را تعریف کنیم ، یعنی منطقه ای که حمل محموله از A به صورت ترکیبی ارزان تر است: از طریق راه آهن و سپس از طریق جاده.

راه حل.هزینه تحویل 1 تن محموله در مسیر AM r n است ، جایی که r = AM ، و در طول مسیر AVM ، معادل 1m + k + r n خواهد بود. ما باید نابرابری مضاعف r n 1m + k + r n را حل کنیم و نحوه توزیع نقاط هواپیما (x ، y) را مشخص کنیم ، که تحویل کالا در مسیر اول یا دوم ارزانتر است.

بیایید معادله خطی را که مرز بین این دو منطقه را تشکیل می دهد ، پیدا کنیم ، یعنی مکان نقاطی که هر دو مسیر برای آنها "به همان اندازه مفید است":

r n = 1m + k + r n

از این شرایط ، r - r = = const را بدست می آوریم.

از این رو ، خط تقسیم بیش از حد است. برای همه نقاط بیرونی این هذلولی ، مسیر اول مفیدتر است ، و برای نقاط داخلی ، مسیر دوم. بنابراین ، هایپربولا منطقه نفوذ ایستگاه B را مشخص می کند. شاخه دوم منطقه نفوذ ایستگاه A را مشخص می کند (محموله از ایستگاه B تحویل داده می شود). بیایید پارامترهای هذلولی خود را بیابیم. محور اصلی آن 2a = است و فاصله بین کانونها (که ایستگاههای A و B هستند) در این حالت 2c = l است.

بنابراین ، شرط احتمال این مشکل ، با رابطه a تعیین می شود< с, будет

این مسأله مفهوم هندسی انتزاعی هایپربول را با مشکل حمل و نقل و اقتصادی پیوند می دهد.

مکان مورد نیاز نقاط مجموعه ای از نقاط است که در داخل شاخه سمت راست هایپروبلا حاوی نقطه B قرار دارد.

6. میدانم " ماشین آلات کشاورزی»زاویه کاستر و رول از ویژگی های مهم عملکرد یک تراکتور در شیب است که پایداری آن را نشان می دهد.

برای سادگی ، ما یک تراکتور چرخدار را در نظر خواهیم گرفت. سطحی که تراکتور روی آن کار می کند (حداقل بخش کوچکی از آن) را می توان یک صفحه (صفحه حرکت) در نظر گرفت. محور طولی تراکتور ، طرح خط مستقیم است که وسط محور جلو و عقب را به صفحه حرکت متصل می کند. زاویه رول جانبی زاویه ای است که با صفحه افقی یک خط مستقیم عمود بر محور طولی تشکیل شده و در صفحه حرکت قرار دارد.

هنگام مطالعه موضوع "خطوط و صفحات در فضا" در درس ریاضیات ، وظایف زیر را در نظر می گیریم:

الف) اگر زاویه افزایش شیب و زاویه انحراف مسیر تراکتور از جهت طولی مشخص باشد ، زاویه شیب طولی تراکتور را که در امتداد شیب حرکت می کند ، بیابید.

ب) حداکثر زاویه مجاز شیب که تراکتور بدون واژگونی از روی آن می تواند بایستد ، زاویه محدود کننده رول جانبی تراکتور نامیده می شود. چه پارامترهای تراکتور برای تعیین زاویه محدود کننده رول جانبی کافی است. چگونه می توان این را پیدا کرد
تزریق؟

7. از ژنراتورهای مستقیم در تجهیزات ساختمانی استفاده می شود. بنیانگذار کاربرد عملی این واقعیت مهندس مشهور روسی ولادیمیر گریگوریویچ شوخوف (1853-1939) است. V.G.Shukhov ساخت دکل ها ، برج ها و تکیه گاه ها ، متشکل از تیرهای فلزی ، واقع در امتداد خطوط راست را انجام داد هایپربلوئید تک ورقه انقلاب.استحکام بالای چنین سازه هایی ، همراه با سبکی ، هزینه ساخت پایین و ظرافت ، استفاده گسترده از آنها را در ساختمان های مدرن تضمین می کند.

8. قوانین حرکت یک بدن جامد رایگان

برای یک بدن آزاد ، همه نوع حرکت به یک اندازه امکان پذیر است ، اما این بدان معنا نیست که حرکت یک بدن آزاد بی نظم است و از هیچ قانونی پیروی نمی کند. برعکس ، حرکت ترجمه ای یک جسم سفت و سخت ، صرف نظر از شکل خارجی آن ، توسط قانون مرکز جرم محدود شده و به حرکت یک نقطه کاهش می یابد و حرکت چرخشی به اصطلاح محورهای اصلی است. اینرسی یا بیضوی اینرسی... بنابراین ، چوبی که به فضای آزاد پرتاب می شود ، یا دانه ای که از مرتب سازی خارج می شود و غیره ، مانند یک نقطه (مرکز جرم) به صورت ترجمه ای حرکت می کند و در همان زمان به دور مرکز جرم می چرخد. به طور کلی ، در حرکت انتقالی ، هر جسم سفت و سختی ، صرف نظر از شکل آن ، یا یک ماشین پیچیده می تواند با یک نقطه (مرکز جرم) و در حرکت چرخشی ، با یک بیضی شکل اینرسی جایگزین شود. ، بردارهای شعاع آن برابر -، جایی که / لحظه اینرسی این جسم نسبت به محورهای عبوری از مرکز بیضی شکل است.

اگر لحظه اینرسی بدن به دلایلی در حین چرخش تغییر کند ، سرعت چرخش نیز متناسب با آن تغییر می کند. به عنوان مثال ، در هنگام پرش از بالای سر ، آکروبات ها به صورت یک توپ فشرده می شوند ، که باعث می شود لحظه اینرسی بدن کاهش یابد و سرعت چرخش افزایش می یابد ، که برای موفقیت پرش ضروری است. به همین ترتیب ، هنگام لغزش افراد ، بازوهای خود را به طرفین دراز می کنند ، که این باعث افزایش لحظه اینرسی و کاهش سرعت چرخش می شود. به همین ترتیب ، لحظه اینرسی چنگک برداشت کننده در مورد محور عمودی در طول چرخش آن در مورد محور افقی متغیر است.

پارابولویید بیضوی

پارابلوئید بیضوی با a = b = 1

پارابولویید بیضوی- سطح توصیف شده با تابعی از فرم

,

جایی که آو بیک علامت سطح توسط خانواده ای از Parabolas های موازی با شاخه هایی به سمت بالا توصیف می شود که رأس آنها یک Parabola را توصیف می کند و شاخه ها نیز به سمت بالا اشاره می کنند.

اگر آ = بسپس یک پارابوئید بیضوی سطحی از انقلاب است که با چرخش یک سهمی در اطراف یک محور عمودی که از راس این سهمی فرعی عبور می کند شکل می گیرد.

پارابولوئید هایپربولیک

پارابولوئید هایپربولیک با a = b = 1

پارابولوئید هایپربولیک(در ساختمان "hypar" نامیده می شود) - سطحی به شکل زین که در یک سیستم مختصات مستطیلی با معادله فرم توصیف شده است.

.

نمای دوم نشان می دهد که پارابولویید هایپربولیک یک سطح تحت کنترل است.

سطح را می توان با حرکت یک سهمی شکل داد که شاخه های آن به سمت پایین ، در امتداد یک سهمی ، که شاخه های آن به سمت بالا هدایت می شوند ، ایجاد می شود ، به شرطی که اولین سهمیه با راس دوم خود در تماس باشد.

پارابولوئیدها در جهان

در تکنولوژی

در هنر

در ادبیات

دستگاه توصیف شده در Hyperboloid مهندس گارین قرار بود باشد پارابولوئید.

بنیاد ویکی مدیا 2010

• ایلون مناخم
• التانگ

ببینید "پارابلوئید بیضوی" در فرهنگ لغت های دیگر چیست:

پارابولوئید الیپتیک فرهنگ لغت دائرclالمعارف بزرگ

پارابولویید بیضوی- یکی از دو نوع پارابولوئید. * * * PARABOLOID ELLIPTIC ELLIPTIC PARABOLOID ، یکی از دو نوع پارابولوئید (به پارابولوئیدها مراجعه کنید) ... فرهنگ لغت دائرclالمعارف

پارابولویید بیضوی- یکی از دو نوع پارابلوئید (به پارابلوئیدها مراجعه کنید) ... دائرclالمعارف بزرگ شوروی

پارابولوئید الیپتیک- سطح غیر بسته از مرتبه دوم. ابتدایی. معادله E. p شکل دارد E. p در یک طرف صفحه Oxy واقع شده است (شکل را ببینید). بخشهای E. p. هواپیماهای موازی با صفحه Oxy بیضی هایی با گریز از مرکز برابر هستند (اگر p ... دانشنامه ریاضیات

پارابولوئید الیپتیک- یکی از دو نوع پارابلوئید ... علوم طبیعی. فرهنگ لغت دائرclالمعارف

پارابولوئید- (یونانی ، از parabole parabola و شباهت eidos). جسمی که از یک سهمی دوار تشکیل شده است. فرهنگ لغات خارجی موجود در زبان روسی. Chudinov AN، 1910. PARABOLOID یک جسم هندسی است که از چرخش یک سهمی شکل گرفته است ، بنابراین ... ... فرهنگ لغات خارجی زبان روسی

پارابولوئید- PARABOLOID ، paraboloid ، شوهر. (به parabola مراجعه کنید) (mat). سطحی مرتبه دوم بدون مرکز. Paraboloid of Revolution (با چرخاندن یک Parabola به دور محور خود تشکیل شده است). پارابولویید بیضوی. پارابولوئید هایپربولیک. فرهنگ لغت توضیحی اوشاکوف ... فرهنگ لغت توضیحی اوشاکوف

پارابولوئید- PARABOLOID ، سطحی که با حرکت یک سهمی به دست می آید ، راس آن در امتداد یک سهمی ثابتی دیگر (با محور تقارن موازی با محور سهمی حرکتی) می لغزد ، در حالی که صفحه آن ، به موازات خود تغییر می کند ، باقی می ماند. .. ... دائرclالمعارف مدرن

پارابولوئید- - نوع سطح مرتبه دوم. یک پارابلوئید را می توان به عنوان یک سطح خارج از مرکز باز (یعنی بدون مرکز تقارن) سطح مرتبه دوم مشخص کرد. معادلات متعارف یک پارابلوئید در مختصات دکارتی: اگر و یک ... ... ویکی پدیا

پارابولوئید-سطح خارج از مرکز خارج از مرتبه دوم. ابتدایی. معادلات P: یک پارابلوئید بیضوی (برای p = q P. چرخش نامیده می شود) و یک پارابولویید هذلولی. ای. ایوانف ... دانشنامه ریاضیات

پارابولویید هذلولی نیز متعلق به سطوح مرتبه دوم است. این سطح را نمی توان با اعمال الگوریتمی با استفاده از چرخش خطی در مورد یک محور ثابت بدست آورد.

یک مدل خاص برای ساختن یک پارابولویید هذلولی استفاده می شود. این مدل شامل دو سه گوش است که در دو صفحه عمود بر یکدیگر قرار گرفته اند.

اجازه دهید Parabola I در هواپیما و بی حرکت باشد. Parabola II یک حرکت پیچیده انجام می دهد:

position موقعیت اولیه آن همزمان با هواپیما است
، و راس parabola با مبدا منطبق است: =(0,0,0);

▫ علاوه بر این ، این سهمی یک حرکت انتقال موازی و بالای آن را ایجاد می کند
مسیری را همزمان با سهمیه اول ایجاد می کند.

▫ دو موقعیت اولیه مختلف Parabola II در نظر گرفته شده است: یکی - شاخه های Parabola به سمت بالا ، دوم - شاخه ها به سمت پایین.

اجازه دهید معادلات را بنویسیم: برای اولین سهمیه اول:
- ثابت ؛ برای دومین سهمیه دوم:
- موقعیت اولیه ، معادله حرکت:
درک این نکته سخت نیست
مختصات دارد:
... از آنجا که لازم است قانون حرکت یک نقطه نمایش داده شود
: این نقطه متعلق به parabola I است ، بنابراین روابط زیر همیشه باید برآورده شوند: =
و
.

به راحتی می توان از روی ویژگی های هندسی مدل ، سهمیه متحرک را مشاهده کرد جارو می کند مقداری سطح در این مورد ، معادله سطح توصیف شده توسط Parabola II به صورت زیر است:

یا
. (1)

شکل سطح حاصله به توزیع علائم پارامتر بستگی دارد
... دو مورد امکان پذیر است:

یک) علائم کمیت ها پو سمنطبق است: سه گوشهای I و II در یک طرف صفحه قرار دارند OXY... بیایید بگیریم: پ = آ 2 و س = ب 2 ... سپس معادله سطح شناخته شده را بدست می آوریم:

→ پارابولویید بیضوی . (2)

2) علائم کمیت ها پو سمتفاوت: parabolas I و II در طرف مقابل هواپیما واقع شده است OXY... بگذار باشد پ = آ 2 و س = - ب 2 ... حال معادله سطح را بدست می آوریم:

→پارابولوئید هذلولی . (3)

اگر مدل سینماتیکی فعل و انفعال دو پارابولا شرکت کننده در حرکت را به خاطر آوریم ، ارائه اشکال هندسی سطح با معادله (3) دشوار نیست.

در شکل ، Parabola I معمولاً با رنگ قرمز نشان داده شده است. فقط مجاورت سطح در مبدأ نشان داده شده است. با توجه به این واقعیت که شکل سطح به وضوح به زین سواره اشاره می کند ، این محله اغلب نامیده می شود - زین اسب .

در فیزیک ، هنگام مطالعه ثبات فرایندها ، انواع تعادل معرفی می شود: پایدار - سوراخ ، محدب به سمت پایین ، ناپایدار - سطح محدب به سمت بالا و متوسط ​​- زین. تعادل نوع سوم نیز به نوع تعادل ناپایدار اطلاق می شود و فقط در خط قرمز (پارابولا I) تعادل امکان پذیر است.

§ 4. سطوح استوانه ای.

هنگام در نظر گرفتن سطوح انقلاب ، ما ساده ترین سطح استوانه ای را شناسایی کرده ایم - یک استوانه چرخش ، یعنی یک استوانه دایره ای.

در هندسه ابتدایی ، یک استوانه با قیاس با تعریف کلی منشور تعریف می شود. کاملاً پیچیده است:

▫ اجازه دهید چند ضلعی مسطح در فضا داشته باشیم
- نشان دادن به عنوان ، و چند ضلعی با آن منطبق است
- نشان دادن به عنوان
;

▫ قابل استفاده برای چند ضلعی
ترجمه موازی حرکت: نقاط
حرکت در امتداد مسیرهای موازی جهت معین ;

▫ اگر حرکت چند ضلعی را متوقف کنید
، سپس صفحه آن
موازی با صفحه ;

▫ سطح یک منشور: مجموعه ای از چند ضلعی ها نامیده می شود ,
– زمینه منشور و متوازی الاضلاع
,
,... – سطح جانبی منشور

که در ما از تعریف ابتدایی منشور برای ساختن تعریف کلی تری از منشور و سطح آن استفاده می کنیم ، یعنی بین موارد زیر تمایز قائل می شویم:

ism منشور نامحدود یک بدن چند وجهی است که توسط لبه ها محدود شده است ,، ... و هواپیماهای بین این لبه ها ؛

pr منشور محدود یک بدن چند وجهی است که توسط لبه ها محدود شده است ,، ... و متوازی الاضلاع
,
، ...؛ سطح جانبی این منشور مجموعه ای از متوازی الاضلاع است
,
، ...؛ پایه های منشوری - مجموعه ای از چند ضلعی ها ,
.

اجازه دهید منشوری نامحدود داشته باشیم: ,، ... بیایید با یک صفحه دلخواه از این منشور عبور کنیم ... بیایید با یک صفحه دیگر از همین منشور عبور کنیم
... در بخش ، ما یک چند ضلعی را دریافت می کنیم
... در حالت کلی ، ما فرض می کنیم که هواپیما
موازی با صفحه نیست ... این بدان معناست که منشور با ترجمه موازی چند ضلعی ساخته نشده است. .

ساختمان پیشنهادی منشور نه تنها شامل منشورهای مستقیم و مایل ، بلکه هر گونه کوتاه شده است.

در هندسه تحلیلی ، ما سطوح استوانه ای را به گونه ای کلی می فهمیم که یک استوانه بدون محدوده شامل یک منشور نامحدود به عنوان یک مورد خاص است: فقط باید فرض کرد که چند ضلعی را می توان با یک خط دلخواه جایگزین کرد ، نه لزوما بسته - راهنما سیلندر. جهت نامیده می شوند generatrix سیلندر.

از همه موارد گفته شده چنین نتیجه می شود: برای تعریف سطح استوانه ای ، لازم است یک خط راهنما و جهت ژنراتریکس مشخص شود.

سطوح استوانه ای بر اساس منحنی صفحه مرتبه دوم خدمت می شوند راهنماها برای ژنراتورها .

در مرحله اولیه مطالعه سطوح استوانه ای ، فرضیات ساده تری را ارائه می دهیم:

▫ اجازه دهید راهنمای سطح استوانه ای همیشه در یکی از صفحات مختصات قرار گیرد.

▫ جهت ژنراتریکس همزمان با یکی از محورهای مختصات ، یعنی عمود بر صفحه ای که دستورالعمل در آن تعریف شده است.

محدودیت های اتخاذ شده منجر به از دست دادن کلیت نمی شود ، زیرا این امکان به دلیل انتخاب بخش ها توسط هواپیماها وجود دارد و
ایجاد اشکال هندسی دلخواه: استوانه های مستقیم ، مایل و کوتاه.

استوانه بیضوی .

اجازه دهید بیضی به عنوان راهنمای استوانه گرفته شود :
واقع در صفحه مختصات

: استوانه بیضوی.

استوانه هایپربولیک .

:

، و جهت ژنراتور محور را تعیین می کند
... در این حالت ، معادله استوانه خود خط است : استوانه هذلولی.

استوانه سهمی .

بگذارید هایپربولا به عنوان راهنمای استوانه در نظر گرفته شود :
واقع در صفحه مختصات
، و جهت ژنراتور محور را تعیین می کند
... در این حالت ، معادله استوانه خود خط است : استوانه سهمی

اظهار نظر: با در نظر گرفتن قوانین کلی برای ساخت معادلات سطوح استوانه ای و همچنین نمونه های خاصی از استوانه های بیضوی ، هیپربولیک و سهمی ارائه شده ، ما توجه می کنیم: ساخت یک استوانه برای هر ژنراتور دیگر ، برای شرایط ساده سازی تصویب شده ، باید هیچ مشکلی ایجاد نمی کند!

اکنون اجازه دهید شرایط کلی تری برای ساخت معادلات سطوح استوانه ای در نظر بگیریم:

▫ راهنمای یک سطح استوانه ای در یک صفحه دلخواه از فضا قرار دارد
;

▫ جهت ژنراتریکس در سیستم مختصات اتخاذ شده به طور خودسرانه.

ما شرایط پذیرفته شده را در شکل ترسیم می کنیم.

surface راهنمای سطح استوانه ای واقع در یک صفحه دلخواه فضا
;

▫ سیستم مختصات
به دست آمده از سیستم مختصات
انتقال موازی ؛

▫ مکان راهنما داخل هواپیما مطلوب ترین: برای منحنی مرتبه 2 ، فرض می کنیم که منشا مختصات است منطبق با مرکز تقارن منحنی مورد بررسی ؛

▫ جهت ژنراتریکس دلخواه (می تواند به هر روش مشخص شود: بردار ، خط مستقیم و غیره).

در موارد زیر ، فرض می کنیم که سیستم های مختصات
و
مطابقت این بدان معناست که گام اول الگوریتم کلی برای ساخت سطوح استوانه ای ، منعکس کننده ترجمه موازی:
→
از قبل اجرا شده است

اجازه دهید یادآوری کنیم که چگونه انتقال موازی در حالت کلی با در نظر گرفتن یک مثال ساده در نظر گرفته می شود.

مثال 6–13 : در سیستم مختصات
مانند:
= 0 معادله این دستورالعمل را در سیستم بنویسید
.

راه حل:

یک) ما یک نقطه دلخواه را نشان می دهیم
: در سیستم
چگونه
، و در سیستم
چگونه
.

2) برابری بردار را می نویسیم:
=
+
... به صورت مختصات ، این را می توان به صورت زیر نوشت:
=
+
... یا به شکل:
=
–
، یا:
=.

3) معادله راهنمای استوانه را می نویسیم در سیستم مختصات
:

پاسخ: معادله راهنمای تبدیل شده: = 0.

بنابراین ، فرض می کنیم که مرکز منحنی نشان دهنده راهنمای استوانه همیشه در مبدأ مختصات سیستم قرار دارد.
داخل هواپیما .

برنج. که در ... نقاشی اولیه هنگام ساخت استوانه.

بیایید یک فرض دیگر را برای ساده سازی مراحل نهایی ساخت سطح استوانه ای انجام دهیم. از آنجا که با استفاده از چرخش سیستم مختصات ، تراز جهت محور آسان است
دستگاه های مختصات
با هواپیما معمولی ، و جهت محورها
و
با محورهای تقارن راهنما ، سپس ما آن را به عنوان موقعیت اولیه راهنما فرض می کنیم ما یک منحنی داریم که در هواپیما قرار دارد
، و یکی از محورهای تقارن آن با محور منطبق است
، و دوم با محور
.

اظهار نظر: از آنجا که اجرای عملیات انتقال موازی و چرخش حول محور ثابت عملیات بسیار ساده است ، مفروضات انجام شده کاربرد الگوریتم توسعه یافته برای ساختن سطح استوانه ای را در حالت کلی محدود نمی کند!

ما دیدیم که هنگام ساختن سطح استوانه ای در مورد راهنمای مورد نظر واقع در هواپیما
، و ژنراتور موازی محور است
، کافی است فقط راهنما را تعریف کنید .

از آنجا که یک سطح استوانه ای را می توان با تعیین هر خط بدست آمده در بخش این سطح توسط یک صفحه دلخواه به طور منحصر به فرد تعیین کرد ، ما الگوریتم کلی زیر را برای حل مسئله می پذیریم:

1 ▫ ... اجازه دهید جهت ژنراتور سطح استوانه ای توسط بردار نشان داده شده است ... ما یک راهنما طراحی خواهیم کرد با معادله داده شده است:
= 0 ، در صفحه ای عمود بر جهت ژنراتریس ، یعنی در هواپیما
... در نتیجه ، سطح استوانه ای در سیستم مختصات مشخص می شود
معادله:
=0.

2 ▫
حول محور
در گوشه
: معنی زاویه
سازگار با سیستم
، و معادله سطح مخروطی به معادله تبدیل می شود:
=0.

3 ▫ ... چرخش سیستم مختصات را اعمال کنید
حول محور
در گوشه
: معنی زاویه از شکل کاملاً مشخص است در نتیجه چرخش ، سیستم مختصات
سازگار با سیستم
، و معادله سطح مخروطی به تبدیل می شود
= 0 این معادله یک سطح استوانه ای است که راهنمای آن داده شده است و تولید در سیستم مختصات
.

مثال زیر اجرای الگوریتم نوشته شده و مشکلات محاسباتی چنین وظایفی را نشان می دهد.

مثال 6–14 : در سیستم مختصات
معادله راهنمای استوانه داده شده است مانند:
= 9 برای استوانه ای که ژنرالهای آن موازی بردار است ، معادله ای ایجاد کنید =(2,–3,4).

R
راه حل:

یک) اجازه دهید راهنمای استوانه را در صفحه ای عمود بر طراحی کنیم ... مشخص است که چنین تحولی یک دایره معین را به بیضی تبدیل می کند ، محورهای آن بزرگ خواهد بود = 9 و کوچک =
.

این شکل طرح یک دایره تعریف شده در یک صفحه را نشان می دهد.
در صفحه مختصات
.

2) نتیجه طراحی یک دایره بیضی است:
= 1 ، یا
... در مورد ما ، اینها عبارتند از:
، جایی که
==.

3
) بنابراین ، معادله سطح استوانه ای در سیستم مختصات
اخذ شده. از آنجا که ، با توجه به شرایط مسئله ، ما باید معادله این استوانه را در سیستم مختصات داشته باشیم
، سپس باید یک تغییر مختصات را که سیستم مختصات را ترجمه می کند اعمال کرد
برای هماهنگی سیستم
به همراه معادله استوانه:
به معادله ای که بر حسب متغیرها بیان شده است
.

4) ما استفاده خواهیم کرد پایه ای همه مقادیر مثلثاتی لازم برای حل مسئله را بنویسید و بنویسید:

==,
==,
==.

پنج) اجازه دهید فرمولهای تبدیل مختصات را هنگام عبور از سیستم بنویسیم
به سیستم
:
(که در)

6) اجازه دهید فرمولهای تبدیل مختصات را هنگام عبور از سیستم بنویسیم
به سیستم
:
(با)

7) جایگزینی متغیرها
از سیستم (B) به سیستم (C) ، و همچنین با در نظر گرفتن مقادیر توابع مثلثاتی مورد استفاده ، می نویسیم:

=
=
.

=
=
.

هشت) باقی مانده است که مقادیر یافت شده را جایگزین کنیم و وارد معادله راهنمای استوانه می شود :
در سیستم مختصات
... پس از تکمیل با دقت همه تغییرات جبری ، ما معادله سطح مخروطی را در سیستم مختصات بدست می آوریم
: =0.

پاسخ: معادله مخروط: = 0.

مثال 6–15 : در سیستم مختصات
معادله راهنمای استوانه داده شده است مانند:
=9, = 1 برای استوانه ای که ژنرالهای آن موازی بردار است ، معادله ای ایجاد کنید =(2,–3,4).

راه حل:

یک) به راحتی می توان فهمید که این مثال با مثال قبلی تفاوت دارد زیرا راهنما به طور موازی 1 به بالا منتقل شده است.

2) این بدان معناست که در روابط (B) باید موارد زیر را در نظر گرفت: =-یک با در نظر گرفتن عبارات سیستم (C) ، نماد متغیر را تصحیح می کنیم :

=
.

3) با اصلاح نماد نهایی معادله برای استوانه از مثال قبلی ، تغییر به راحتی در نظر گرفته می شود:

پاسخ: معادله مخروط: = 0.

اظهار نظر: به آسانی می توان دریافت که مشکل اصلی در تحولات متعدد سیستم های مختصات در مشکلات سطوح استوانه ای است دقت و تحمل در ماراتن های جبری: زنده باد نظام آموزشی اتخاذ شده در کشور دردمند ما!

ارتفاع پارابلوئید را می توان با فرمول تعیین کرد

حجم پارابلوئید که به پایین دست می زند برابر با نصف حجم یک استوانه با شعاع پایه R و ارتفاع H است ، همین حجم توسط فضای W 'زیر پارابولوئید اشغال شده است (شکل 4.5a)

شکل 4.5. نسبت حجم ها در یک پارابلوئید که به پایین دست می زند.

Wп - حجم پارابولوئید ، W ' - حجم زیر پارابولوئید ، Hп - ارتفاع پارابولوئید

شکل 4.6. نسبت حجم ها در پارابلوئید که لبه های سیلندر را لمس می کند ارتفاع پارابولوئید است ، R شعاع ظرف است ، Wl حجم زیر ارتفاع مایع در ظرف قبل از شروع چرخش است ، z 0 موقعیت راس پارابلوئید است ، H ارتفاع مایع در ظرف قبل از شروع چرخش است.

در شکل 4.6a ، سطح مایع در سیلندر قبل از شروع چرخش H. حجم مایع Wl قبل و بعد از چرخش حفظ می شود و برابر است با مجموع حجم Wc استوانه با ارتفاع z 0 به علاوه حجم مایع زیر پارابلوئید ، که برابر حجم پارابولوئید Wp با ارتفاع Hp است

اگر پارابلوئید لبه بالای سیلندر را لمس کند ، ارتفاع مایع در سیلندر قبل از شروع چرخش Н ارتفاع پارابلوئید Нп را به دو قسمت مساوی تقسیم می کند ، نقطه پایین (بالا) پارابلوئید در رابطه قرار دارد. به پایه (شکل 4.6c)

علاوه بر این ، ارتفاع H پارابلوئید را به دو قسمت تقسیم می کند (شکل 4.6c) ، که حجم آنها برابر W2 = W1 است. از برابری حجم حلقه سهمی W 2 و جام سهموی W 1 ، شکل 4.6c

هنگامی که سطح پارابولوئید از ته ظرف عبور می کند (شکل 4.7) W 1 = W 2 = 0.5W حلقه

شکل 4.7 حجم و ارتفاع زمانی که سطح پارابولوئید از زیر استوانه عبور می کند

ارتفاعات در شکل 4.6

حجم های شکل 4.6.

محل سطح آزاد در ظرف

شکل 4.8. سه مورد استراحت نسبی در حین چرخش

1. اگر رگ باز است ، Po = Ratm (شکل 4.8a). رأس پارابلوئید در حین چرخش به زیر سطح اولیه H می افتد و لبه ها بالاتر از سطح اولیه قرار می گیرند ، موقعیت رأس

2. اگر ظرف به طور کامل پر شود ، با یک درپوش پوشانده شود ، سطح آزاد نداشته باشد ، تحت فشار بیش از حد Po> Ratm ، قبل از چرخش سطح (PP) ، که R0 = Ratm بالاتر از سطح درپوش در یک ارتفاع h 0i = M / ρg ، H 1 = H + M / ρg.

3. اگر ظرف به طور کامل پر شود ، تحت خلاء Po قرار دارد<Ратм, до вращения поверхность П.П., на которой Ро=Ратм будет находиться под уровнем крышки на высоте h 0и =-V/ρg, Н 2 =Н-V/ρg ,

4.7 چرخش با سرعت زاویه ای بالا (شکل 4.9)

وقتی یک ظرف با مایع با سرعت زاویه ای بالا می چرخد ​​، می توان از نیروی گرانش در مقایسه با نیروهای گریز از مرکز غفلت کرد. قانون تغییر فشار در مایع را می توان از فرمول بدست آورد

(4.22),

سطوح تراز استوانه هایی با محور مشترک تشکیل می دهند که ظرف در اطراف آنها می چرخد. اگر ظرف قبل از شروع چرخش کاملاً پر نشده باشد ، فشار را فشار دهید P 0 در طول شعاع عمل خواهد کرد r = r 0 ، به جای عبارت (4.22) ما خواهیم داشت

جایی که ما g (z 0 - z) = 0 را می گیریم ،

برنج. 4.9 چیدمان سطوح انقلاب در غیاب گرانش.

شعاع سطح داخلی با H و h شناخته شده