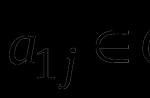ให้สนาม NSที่มีอยู่ในสนาม NSและ NS- องค์ประกอบ NSไม่ได้เป็นเจ้าของ NS... พิจารณาช่องที่เล็กที่สุด NS(NS) ที่มีองค์ประกอบทั้งหมดจาก NSและ NS... องค์ประกอบทั้งหมดของมุมมองเป็นของ NS(NS). ลองพิจารณาสองกรณี
สิ้นสุดฟิลด์
ทฤษฎีบท 4.2 จำนวนองค์ประกอบของสนามจำกัดคือ p n โดยที่ p เป็นจำนวนเฉพาะ
การพิสูจน์... เนื่องจากสนาม P นั้นจำกัด ลักษณะของมันจึงไม่ใช่ศูนย์ ให้ p เป็นคุณลักษณะของมัน ฟิลด์ P สามารถมองได้ว่าเป็นเวคเตอร์สเปซส่วน Z p ให้ v 1,…, v n แสดงถึงฐาน P. องค์ประกอบใดๆ ของฟิลด์ P จะมีลักษณะเฉพาะโดยพิกัด (x 1,…, x n) ในเกณฑ์นี้ แต่ละพิกัดใช้ค่า p ดังนั้น จำนวนของชุดพิกัดที่แตกต่างกัน และด้วยเหตุนี้องค์ประกอบของฟิลด์ P จึงเท่ากับ p n
บทแทรก 4.1 ในด้านคุณลักษณะ NS ![]() .
.
การพิสูจน์. ![]() , โดยที่หลายหลากของการเกิดขึ้นขององค์ประกอบอยู่ที่ไหน ปริมาณหารด้วย .ไม่ได้ NSเฉพาะในกรณี ผม = 0;NS.เนื่องจาก pe = 0, แล้ว
, โดยที่หลายหลากของการเกิดขึ้นขององค์ประกอบอยู่ที่ไหน ปริมาณหารด้วย .ไม่ได้ NSเฉพาะในกรณี ผม = 0;NS.เนื่องจาก pe = 0, แล้ว ![]() .
.
ทฤษฎีบท 4.3 สำหรับ n และไพรม์ p ใดๆ จะมีฟิลด์ของคำสั่ง p n
เราขยาย Z p เพื่อให้ฟิลด์ผลลัพธ์มีรากของพหุนามทั้งหมด พหุนามไม่มีรากหลายตัว เนื่องจากอนุพันธ์ของมันคือ –1 ให้ M แทนเซตรากของพหุนาม ง่ายต่อการตรวจสอบว่า M เป็นฟิลด์และจำนวนองค์ประกอบเท่ากับ p n
ทฤษฎีบท 4.4 ฟิลด์คำสั่งไม่ซ้ำกันจนถึง isomorphism
การพิสูจน์.
เนื่องจากจำนวนขององค์ประกอบของสนามจึงมีลักษณะเท่ากัน ดังนั้น สาขาใดๆ NSสามารถดูได้ว่าเป็นส่วนขยายของวงแหวนที่เหลือ กลุ่มการคูณของฟิลด์ () มีลำดับ ดังนั้น ค่าใดๆ ก็เป็นจริง ดังนั้นองค์ประกอบทั้งหมดของสนามจึงเป็นรากของสมการ
ทฤษฎีบท 4.5. กลุ่มรากทวีคูณ NS- องศาที่ 1 ในสนาม P เป็นวงกลม
การพิสูจน์.ปล่อยให้เป็น NSลักษณะสนาม NS... ถ้าอย่างนั้น  และดังนั้น เซตของรูทของสมการจึงตรงกับเซตของรูทของดีกรี โดยไม่ทำลายลักษณะทั่วไปก็สามารถพิจารณาได้ ก็เพียงพอแล้วที่จะดำเนินการพิสูจน์กรณีที่รากทั้งหมด NS- กำลังที่ 1 อยู่ในสนาม NS... มิฉะนั้น เราจะขยายฟิลด์และใช้ข้อเท็จจริงที่ว่ากลุ่มย่อยใดๆ ของกลุ่มไซคลิกนั้นเป็นแบบวน เพราะว่า
และดังนั้น เซตของรูทของสมการจึงตรงกับเซตของรูทของดีกรี โดยไม่ทำลายลักษณะทั่วไปก็สามารถพิจารณาได้ ก็เพียงพอแล้วที่จะดำเนินการพิสูจน์กรณีที่รากทั้งหมด NS- กำลังที่ 1 อยู่ในสนาม NS... มิฉะนั้น เราจะขยายฟิลด์และใช้ข้อเท็จจริงที่ว่ากลุ่มย่อยใดๆ ของกลุ่มไซคลิกนั้นเป็นแบบวน เพราะว่า ![]() มีเพียงรูทเดียวเท่ากับศูนย์ แล้วจึงเท่ากับจำนวนรูท NS- ยกกำลังที่ 1 เท่ากับ NS... พิจารณาสามกรณี:
มีเพียงรูทเดียวเท่ากับศูนย์ แล้วจึงเท่ากับจำนวนรูท NS- ยกกำลังที่ 1 เท่ากับ NS... พิจารณาสามกรณี:
1. NS- จำนวนเฉพาะ. จากนั้นกลุ่มรากก็จะเป็นระเบียบ NSและด้วยเหตุนี้ วัฏจักร
2. - กำลังของจำนวนเฉพาะ หารากของสมการที่ไม่ใช่รากของสมการ ลำดับองค์ประกอบเป็นตัวหารของลำดับกลุ่ม NSและไม่ใช่ตัวหาร ดังนั้นคำสั่งคือ NSและกลุ่มเป็นวัฏจักร
3. ให้. ให้เราแสดงโดยองค์ประกอบกำเนิดของกลุ่มวัฏจักรของรากระดับ 1 มาใส่กัน เหนี่ยวนำ on kแสดงว่าลำดับเท่ากัน ที่ k= 1 ข้อความนั้นชัดเจน มาพิสูจน์กัน k-หนึ่ง. ลำดับของรายการคือ ตัวหารร่วมที่ยิ่งใหญ่ที่สุด NSและเท่ากับ 1 จึงมีตัวเลข ยูและ วี, อะไร . เนื่องจาก และ ลำดับขององค์ประกอบนั้นหารด้วย NSและต่อ นอกจากนี้ จากความเท่าเทียมกัน ลำดับขององค์ประกอบเป็นตัวหาร ทฤษฎีบทได้รับการพิสูจน์แล้ว
ทฤษฎีกาลัวส์
สนาม NSเรียกว่า การขยายขอบเขตจำกัด NS, ถ้า NSเป็นสเปซเชิงเส้นตรงที่มีมิติมากกว่า NS... มิติของพื้นที่เรียกว่าระดับการขยายตัว
ส่วนขยายฟิลด์พีชคณิตใด ๆ NSมีขอบเขต ดีกรีเท่ากับดีกรีของพหุนามลดทอนไม่ได้
ทฤษฎีบท 5.1 การขยายตัวขั้นสุดท้าย ยูทุ่งนา NSซึ่งเป็นส่วนต่อขยายสุดท้ายของสนาม NS, เป็นนามสกุลสุดท้าย NS... นอกจากนี้ระดับการขยายตัว ยูเกิน NSเท่ากับผลคูณของดีกรีการขยายตัว
การพิสูจน์... เกือบจะชัดเจน
องค์ประกอบของสนาม NSเรียกว่าพีชคณิตมากกว่า NSถ้าเป็นรากของพหุนามบางตัวทับ NS.
องค์ประกอบทั้งหมดของส่วนขยายสุดท้าย NSพีชคณิตมากกว่า NS.
การขยายแบบจำกัดจำนวนใด ๆ สามารถทำได้โดยการเพิ่มส่วนขยายพีชคณิตจำนวนจำกัด
ทฤษฎีบท 5.2 การขยายสนามแบบจำกัดใดๆ NSลักษณะ 0 เป็นส่วนขยายอย่างง่าย
การพิสูจน์ไม่ชัดเจน
การขยายตัวขั้นสุดท้าย NSเรียกว่าการขยายตัวปกติ NSถ้าจากข้อเท็จจริงที่ว่าพหุนามลดไม่ได้มากกว่า NSมีใน NSราก มันจะติดตามการย่อยสลายของมันไปเป็นปัจจัยเชิงเส้น เป็นที่ชัดเจนว่าการขยายปกติของสนามที่มีลักษณะเฉพาะ 0 คือสนามการสลายตัวของพหุนาม การสนทนาก็เป็นจริงเช่นกัน ฟิลด์การสลายตัวของพหุนามเป็นส่วนขยายปกติ
automorphism ของสนามคือการทำแผนที่ isomorphic ลงบนตัวมันเอง
กลุ่ม Galois ของส่วนขยายปกติ NSทุ่งนา NSเป็นกลุ่มของ automorphisms ของสนาม NSรักษาองค์ประกอบของสนาม NS.
ทฤษฎีบท 5.3 สู่ทุกสนามกลาง ยูมีกลุ่มย่อยของกลุ่ม Galois ที่สอดคล้องกันคือคอลเล็กชั่น automorphisms เหล่านั้นที่ไม่เปลี่ยนแปลงองค์ประกอบ ฟิลด์ถูกกำหนดโดยกลุ่มย่อยโดยเฉพาะ
การขยายสนามพีชคณิต- - ฟิลด์ส่วนขยายความปลอดภัยข้อมูลหัวข้อ EN ... คู่มือนักแปลทางเทคนิค
ฟิลด์ E ที่มีฟิลด์ K ที่กำหนดเป็นฟิลด์ย่อย ประเภทของส่วนขยาย ส่วนขยายเกี่ยวกับพีชคณิตคือส่วนขยายทั้งหมดที่มีองค์ประกอบที่เป็นพีชคณิตมากกว่า K นั่นคือองค์ประกอบใดๆ ที่เป็นรากของพหุนามบางตัว f (x) c ... ... Wikipedia
การขยายพีชคณิตของสนาม EQ K ที่ปกติและแยกออกได้ ภายใต้เงื่อนไขเหล่านี้ E จะมีจำนวน automorphisms มากกว่า K (ถ้า E เป็นจำนวนจำกัด จำนวน automorphisms ก็จะมีจำกัดและเท่ากับระดับของการขยาย) ... ... Wikipedia
เซมิกรุ๊ป A คือเซมิกรุ๊ป S ที่มี A เป็นกลุ่มย่อย โดยปกติเรากำลังพูดถึงส่วนขยายของเซมิกรุ๊ป A ที่เกี่ยวข้องกับ Atemi หรือเงื่อนไขอื่นๆ การพัฒนามากที่สุดคือทฤษฎีของเซมิกรุ๊ปในอุดมคติ (เซมิกรุ๊ปที่มี AV เป็น ... ... สารานุกรมคณิตศาสตร์
สมการของรูปแบบที่เป็นพหุนามดีกรีที่ n ในตัวแปรตั้งแต่หนึ่งตัวขึ้นไป ก. ณ. ด้วยชื่อที่ไม่รู้จัก สมการของรูปแบบ: ในที่นี้ n คือจำนวนเต็มที่ไม่ติดลบ เรียกว่า สัมประสิทธิ์ของสมการและเป็นข้อมูล hnaz ไม่รู้จักและเป็น ... ... สารานุกรมคณิตศาสตร์
เขตข้อมูล k พีชคณิต ส่วนขยายของสนาม k ซึ่งเป็นสนามปิดเชิงพีชคณิต ส่วนขยายดังกล่าวสำหรับฟิลด์ k ใดๆ มีอยู่และถูกกำหนดขึ้นเฉพาะกับ isomorphism ก.ซ. ฟิลด์ของจำนวนจริงคือฟิลด์ของจำนวนเชิงซ้อน (ดู ... ... สารานุกรมคณิตศาสตร์
ส่วนขยายปกติคือการขยายพีชคณิตของสนาม EQ K ซึ่งทุกพหุนามที่ลดค่าไม่ได้ (x) เหนือ K ที่มีอย่างน้อยหนึ่งรูตใน E จะถูกย่อยสลายใน E เป็นปัจจัยเชิงเส้น คำจำกัดความเทียบเท่า: ถ้า KÌ EÌ K * โดยที่ K * ... ... Wikipedia
ส่วนขยายที่แยกได้คือส่วนขยายเกี่ยวกับพีชคณิตของเขตข้อมูลที่ประกอบด้วยองค์ประกอบที่แยกได้ นั่นคือองค์ประกอบดังกล่าว α ซึ่งเป็นตัวทำลายขั้นต่ำ f (x) เหนือ K ซึ่งไม่มีรากหลายราก อนุพันธ์ f (x) ต้องเป็นไปตามข้างต้น ... ... Wikipedia
ส่วนขยายของฟิลด์ในลักษณะที่ E มีมิติจำกัดเหนือ K เป็นสเปซเวกเตอร์ มิติของสเปซเวกเตอร์ E ส่วน K เรียกว่า ดีกรีของการขยาย และแสดงแทนด้วย คุณสมบัติของนามสกุลจำกัด นามสกุลจำกัดเป็นพีชคณิตเสมอ ใน ... ... Wikipedia
ฟิลด์นี้เป็นส่วนขยายเกี่ยวกับพีชคณิต L ของฟิลด์ K ซึ่งเป็นไปตามเงื่อนไขที่เทียบเท่าข้อใดข้อหนึ่งต่อไปนี้: 1) การฝังฟิลด์ L ใดๆ ลงในพีชคณิต การปิดสนาม K คือ automorphism ของสนาม L; 2) L คือสนามการสลายตัวของพหุนามบางตระกูลที่มี ... ... สารานุกรมคณิตศาสตร์
ส่วนขยายฟิลด์พีชคณิต
บทนำ.
ในมหาวิทยาลัยการสอน มีการแนะนำโปรแกรมสำหรับหลักสูตรรวมในทฤษฎีพีชคณิตและตัวเลข เป้าหมายหลักของหลักสูตรนี้คือการศึกษาระบบพีชคณิตขั้นพื้นฐานและการศึกษาวัฒนธรรมเกี่ยวกับพีชคณิตซึ่งจำเป็นสำหรับครูในอนาคตเพื่อความเข้าใจอย่างลึกซึ้งเกี่ยวกับเป้าหมายและวัตถุประสงค์ของทั้งหลักสูตรคณิตศาสตร์ของโรงเรียนหลักและวิชาเลือกของโรงเรียน
ในความเห็นของเรา แนวทางที่เหมาะสมที่สุดคือการนำองค์ประกอบของพีชคณิตนามธรรมสมัยใหม่มาใช้ในการสอนของโรงเรียน
กระบวนการพีชคณิตของคณิตศาสตร์ซึ่งเริ่มขึ้นในศตวรรษที่ 20 ไม่หยุด และสิ่งนี้ทำให้เกิดความพยายามที่จะแนะนำแนวคิดเกี่ยวกับพีชคณิตขั้นพื้นฐานในการศึกษาคณิตศาสตร์ของโรงเรียน
ความลึกทางคณิตศาสตร์และขอบเขตการประยุกต์ใช้เขตข้อมูลที่กว้างผิดปกติรวมกับความเรียบง่ายของข้อกำหนดพื้นฐาน - แนวคิดของเขตข้อมูล สามารถกำหนดและพิสูจน์ทฤษฎีบทที่สำคัญจำนวนหนึ่งได้โดยมีแนวคิดเริ่มต้นในด้านทฤษฎีเซต ดังนั้นทฤษฎีภาคสนามจึงเหมาะสมที่สุดที่จะแสดงตัวอย่างคณิตศาสตร์สมัยใหม่ให้เด็กนักเรียนเห็น
นอกจากนี้ การศึกษาองค์ประกอบของทฤษฎีภาคสนามยังมีประโยชน์สำหรับเด็กนักเรียน มีส่วนช่วยในการเติบโตทางปัญญา ซึ่งแสดงออกถึงการพัฒนาและเสริมสร้างแง่มุมต่างๆ ของความคิด คุณภาพ และลักษณะบุคลิกภาพ ตลอดจนส่งเสริมความสนใจของนักเรียน คณิตศาสตร์และวิทยาศาสตร์
1. การขยายฟิลด์พีชคณิตอย่างง่าย
1.1 การขยายฟิลด์อย่างง่าย
ให้ P [x] เป็นวงแหวนพหุนามใน x เหนือสนาม P โดยที่ P เป็นฟิลด์ย่อยของ F จำได้ว่าองค์ประกอบ a ของสนาม F เรียกว่าพีชคณิตเหนือสนาม P ถ้า a เป็นรากของพหุนามบวก องศาจาก P [x]
คำนิยาม. ให้พี่< F и a0F. Простым расширением поля P с помощью элемента a называется наименьшее подполе поля F, содержащее множество Р и элемент a. Простое расширение P с помощью a обозначается через P (a), основное множество поля P (a) обозначается через Р(a).
ให้ a0F, P [x] เป็นวงแหวนของพหุนามใน x และ
P [x] = (f (a) * f0P [x]),
นั่นคือ P [a] คือเซตของนิพจน์ทั้งหมดของรูปแบบ a 0 + a 1 a + ... + a n a n โดยที่ 0, a 1, ... a n 0P และ n เป็นจำนวนธรรมชาติใดๆ
มันง่ายที่จะเห็นว่าพีชคณิต + P [a], +, -,., 1, - วงแหวนย่อยของฟิลด์ P (a) - เป็นวงแหวน วงแหวนนี้แสดงด้วยสัญลักษณ์ P [a]
ทฤษฎีบท 1.1 ให้ P [x] เป็นวงแหวนของพหุนามใน x ส่วน P และ P (a) ส่วนขยายอย่างง่ายของสนาม P ให้ y เป็นการจับคู่จาก P [x] ไปยัง P [a] โดยที่ y (f) = f (a) สำหรับ f ใด ๆ จาก P [x] แล้ว:
(a) สำหรับ a จาก P y (a) = a;
(c) y เป็น homomorphism ของวงแหวน P [x] บนวงแหวน P [a];
(d) Ker y = (f0P [x] * f (a) = 0);
(f) วงแหวนผลหาร P [x] / Ker y เป็นไอโซมอร์ฟิคของวงแหวน P [a]
การพิสูจน์. ข้อความ (a) และ (b) เป็นไปตามคำจำกัดความของ y โดยตรง การทำแผนที่ y รักษาการทำงานหลักของวงแหวน P [x] เนื่องจากสำหรับ f และ g จาก P [x]
y (f + g) = f (a) + g (a), y (fg) = f (a) g (a), y (1) = 1
คำชี้แจง (d) ตามมาโดยตรงจากคำจำกัดความของการทำแผนที่ y
เนื่องจาก y เป็น homomorphism ของวงแหวน P [x] บน P [a] ดังนั้น วงแหวนผลหาร P [x] / Ker y จึงเป็นไอโซมอร์ฟิคของวงแหวน P [a]
ข้อพิสูจน์ 1.2. ปล่อยให้ a เป็นองค์ประกอบเหนือธรรมชาติเหนือสนาม P จากนั้นวงแหวนพหุนาม P [x] จะเป็นไอโซมอร์ฟิคสำหรับวงแหวน P [a]
การพิสูจน์. เนื่องจากการมีชัยของ a ส่วน P, Kery = (0) ดังนั้น P [x] / (0) - P [a] ยิ่งกว่านั้น วงแหวนผลหารของวงแหวน P [x] โดยอุดมคติเป็นศูนย์นั้นมีค่า isomorphic ถึง P [x] ดังนั้น P [x] - P [a]
1.2 พหุนามขั้นต่ำขององค์ประกอบเกี่ยวกับพีชคณิต
ให้ P [x] เป็นวงแหวนพหุนามเหนือสนาม P
คำนิยาม. อนุญาต a เป็นองค์ประกอบพีชคณิตเหนือสนาม P. พหุนามน้อยที่สุดขององค์ประกอบ a ส่วน P เป็นพหุนามที่ทำให้เป็นมาตรฐานจาก P [x] ที่มีดีกรีน้อยที่สุดซึ่งมีรากเป็น a ดีกรีของพหุนามน้อยที่สุดเรียกว่า ดีกรีขององค์ประกอบ a ส่วน P
เป็นเรื่องง่ายที่จะเห็นว่าสำหรับทุกองค์ประกอบพีชคณิตบน P มีพหุนามน้อยที่สุด
ข้อเสนอ 1.3. ถ้า a เป็นองค์ประกอบเชิงพีชคณิตเหนือสนาม P และ g และ j เป็นพหุนามน้อยที่สุดบน P ดังนั้น g = j
การพิสูจน์. องศาของพหุนามน้อยที่สุด g และ j ตรงกัน ถ้า g ¹ j แล้วองค์ประกอบ a (ของดีกรี n ส่วน P) จะเป็นรากของพหุนาม g - j ซึ่งระดับนั้นน้อยกว่าดีกรีของพหุนาม j (น้อยกว่า n) ซึ่งเป็นไปไม่ได้ ดังนั้น g = j
ทฤษฎีบท 1.4 ให้ a เป็นองค์ประกอบพีชคณิตของดีกรี n เหนือสนาม P (aóP) และก. พหุนามน้อยที่สุดบน P แล้ว:
(a) พหุนาม g ลดไม่ได้ในวงแหวน P [x];
(b) ถ้า f (a) = 0 โดยที่ f 0 P [x] จากนั้น g หาร f;
(c) วงแหวนผลหาร P [x] / (g) เป็นไอโซมอร์ฟิคของวงแหวน P [a];
(d) P [x] / (g) เป็นฟิลด์;
(f) วงแหวน P [a] เกิดขึ้นพร้อมกับสนาม P (a)
การพิสูจน์. สมมติว่าพหุนาม g ลดลงได้ในวงแหวน P [x] นั่นคือ มีพหุนาม j และ h อยู่ใน P [x] ในลักษณะที่ว่า
g = jh, 1 £ deg j, องศา h จากนั้น g (a) = j (a) h (a) = 0 เนื่องจาก P (a) เป็นสนาม ดังนั้น j (a) = О หรือ h (a) = 0 ซึ่งเป็นไปไม่ได้ เนื่องจากโดยสมมติฐาน ระดับขององค์ประกอบ a ส่วน P เท่ากับ n สมมติว่า f 0 P [x] และ f (a) = 0 โดยสมมติฐาน g (a) = 0 ดังนั้น f และ g ไม่สามารถ coprime ได้ เนื่องจาก g ลดไม่ได้ g จึงหาร f ให้ j เป็น homomorphism ของวงแหวน P [x] บนวงแหวน P [a] (y (f) = f (a) สำหรับ f ใดๆ จาก P [x]) ที่พิจารณาในทฤษฎีบท 2.1 โดยอาศัยอำนาจตาม (b) เคอร์เนลของ homomorphism y ประกอบด้วยทวีคูณของพหุนาม g นั่นคือ เคอร์ y = (g) ดังนั้น วงแหวนผลหาร P = P [x] / (g) จึงเป็นไอโซมอร์ฟิคของวงแหวน P [a] เนื่องจาก P [a] ÌP (a) ดังนั้น P [a] จึงเป็นโดเมนของความซื่อสัตย์ เนื่องจาก P @ P [a] ดังนั้นวงแหวนผลหาร P จึงเป็นโดเมนของความสมบูรณ์ เราต้องแสดงให้เห็นว่าองค์ประกอบใด ๆ ที่ไม่ใช่ศูนย์ f จาก P สามารถแปลงกลับเป็น P ได้ ให้ f เป็นองค์ประกอบของ coset f ตั้งแต่ f ¹ 0 จากนั้น f (a) ¹0; ดังนั้นพหุนาม g จึงไม่หารพหุนาม f เนื่องจากพหุนาม g นั้นลดทอนไม่ได้ มันจึงตามมาด้วยว่าพหุนาม f และ g เป็น coprime ดังนั้นใน P [x] มีพหุนาม u และ v เช่นนั้น uf + vg = 1 นี่แสดงถึงความเท่าเทียมกัน uf = 1 ซึ่งแสดงให้เห็นว่าองค์ประกอบ f สามารถกลับด้านได้ในวงแหวน P ดังนั้นเราจึงกำหนดได้ว่าวงแหวนผลหาร P เป็นสนาม โดยอาศัยอำนาจตาม (c) และ (d) P [a] เป็นสนาม ดังนั้น P (a) ÌP [a] นอกจากนี้ เป็นที่ชัดเจนว่า P [a] ÌP (a) ดังนั้น P [a] = P (a) ดังนั้นวงแหวน P [a] จึงเกิดขึ้นพร้อมกับสนาม P (a) 1.3 การสร้างส่วนขยายฟิลด์พีชคณิตอย่างง่าย ทฤษฎีบท 1.5 ให้ a เป็นองค์ประกอบของดีกรีบวก n พีชคณิตเหนือสนาม P จากนั้นองค์ประกอบใดๆ ของสนาม P (a) สามารถแสดงได้อย่างเฉพาะเจาะจงเป็นการรวมเชิงเส้นของ n องค์ประกอบ 1, a, ..., a n-1 พร้อมสัมประสิทธิ์จาก P การพิสูจน์. ให้ b เป็นองค์ประกอบใดๆ ของสนาม P (a) โดยทฤษฎีบท 1.4, P (a) = P [a]; จึงมีอยู่ใน P [x] พหุนาม f เช่นนั้น ให้ g เป็นพหุนามน้อยที่สุดสำหรับ a ส่วน P; โดยสมมติฐานของทฤษฎีบทระดับของมันเท่ากับ n โดยทฤษฎีบทการหารด้วยเศษเหลือมีอยู่ในพหุนาม P [x] h และ r เช่นนั้น (2) f = gh + r โดยที่ r = 0 หรือ der r< der g = n , т. е. r=c 0 +c 1 x +…c n -1 x n -1 (c i 0P). Полагая в (2) x = а и
учитывая равенство (1), имеем (3) b = c 0 + c 1 a + ... c n -1 a n-1 ให้เราแสดงให้เห็นว่าองค์ประกอบ b สามารถแทนค่าได้โดยไม่ซ้ำกันเป็นการรวมเชิงเส้นขององค์ประกอบ 1, a, ..., a n-1 ปล่อยให้เป็น (4) b = d 0 + d 1 a +… d n -1 a n-1 (d i 0 P) ประสิทธิภาพดังกล่าว พิจารณาพหุนาม j j = (c 0 - d 0) + (c 1 - d i.) x + ... ... + (ด้วย n-1 –d n -1) x n -1 กรณีที่ระดับของ j น้อยกว่า n เป็นไปไม่ได้ เนื่องจากโดยอาศัยอำนาจตาม (3) และ (4) j (a) = 0 และระดับของ j น้อยกว่าระดับของ g กรณีเดียวที่เป็นไปได้คือเมื่อ j = 0, นั่นคือ, โดยที่ 0 = d 0 ... ... โดยที่ n-1 = d n-1 ดังนั้น องค์ประกอบ b จึงสามารถแทนค่าได้โดยไม่ซ้ำกันเป็นการรวมเชิงเส้นขององค์ประกอบ 1, a,…, a n-1 1.4 การยกเว้นจากความไม่ลงตัวของพีชคณิตในตัวส่วนของเศษส่วน ปัญหาของการกำจัดความไม่มีเหตุผลเกี่ยวกับพีชคณิตในตัวส่วนของเศษส่วนมีดังนี้ อนุญาต a เป็นองค์ประกอบพีชคณิตของดีกรี n> 1 เหนือสนาม P; f และ h เป็นพหุนามจากวงแหวนของพหุนาม P [x] และ h (a) ¹0 จำเป็นต้องเป็นตัวแทนขององค์ประกอบ f (a) / h (a) 0P (a) ในรูปแบบของการรวมเชิงเส้นของพลังขององค์ประกอบ a นั่นคือในรูปแบบ j (a) ปัญหานี้แก้ไขได้ดังนี้ ให้ g เป็นพหุนามน้อยที่สุดสำหรับ a ส่วน P เนื่องจากตามทฤษฎีบท 1.4 พหุนามจึงลดทอนไม่ได้ส่วน P และ h (a) ¹ 0, g ไม่หาร h และด้วยเหตุนี้พหุนาม h และ g จึงเป็น coprime ดังนั้นจึงมีพหุนาม u และ v ใน P [x] เช่นนั้น เนื่องจาก g (a) = 0 ตามด้วย (1) that u (a) g (a) = 1, 1 / h (a) = u (a) ดังนั้น f (a) / h (a) = f (a) u (a) และ f, u 0P [x] และ f (a) u (a) 0P [a] ดังนั้นเราจึงกำจัดความไร้เหตุผลในตัวส่วนของเศษส่วน f (a) / h (a) กำจัดความไร้เหตุผลในตัวส่วนของเศษส่วน พหุนาม p (x) และ g (x) = - x 2 + x + 1 เป็น coprime ดังนั้นจึงมีพหุนาม j และ y อยู่เช่นว่า ในการหา j และ y เราใช้อัลกอริทึมของ Euclid กับพหุนาม p และ g: X 3 -2 -x 2 + x + 1 -x 2 + x + 1 2x-1 x 3 -x 2 -x -x-1 -x 2 + 1 / 2x -1 / 2x + 1/4 x 2 -x-1 1/2x-1/4 ดังนั้น, p = ก. (-x-1) + (2x-1), ก. = (2x-1) (- 1 / 2x + 1/4) +5/4 หาได้ที่ไหน (2x-1) = p + g (x + 1), 5/4 = g- (p + g (x + 1)) (- 1 / 2x + 1/4) p1 / 5 (2x-1) + ก. (4/5 + 1/5 (2x 2 + x-1)) = 1, p1 / 5 (2x-1) + ก. (2 / 5x 2 + 1 / 5x + 3/5) = 1 ดังนั้น, y (x) = (2 / 5x 2 + 1 / 5x + 3/5) เพราะเหตุนี้ 2. การขยายพีชคณิตแบบผสมของสนาม 2.1. สุดยอดการขยายสนาม ให้ P เป็นฟิลด์ย่อยของ F จากนั้นเราสามารถถือว่า F เป็นเวคเตอร์สเปซส่วน P นั่นคือ พิจารณาเวคเตอร์สเปซ + F, +, (w l 1l 0P) โดยที่ w l คือการดำเนินการของการคูณองค์ประกอบจาก F ด้วยสเกลาร์ l0P คำนิยาม. ส่วนขยาย F ของฟิลด์ P เรียกว่า finite ถ้า F เป็นเวคเตอร์สเปซเหนือ P มีมิติจำกัด มิตินี้แสดงโดย ข้อเสนอ 2.1. ถ้า a เป็นองค์ประกอบพีชคณิตของดีกรี n ส่วน P แล้ว = n ข้อเสนอนี้ติดตามโดยตรงจากทฤษฎีบท 1.5 คำนิยาม. ส่วนขยาย F ของฟิลด์ P เรียกว่าพีชคณิต ถ้าทุกองค์ประกอบของ F เป็นพีชคณิตมากกว่า P ทฤษฎีบท 2.2. ส่วนขยายใด ๆ F ของฟิลด์ P คือพีชคณิตส่วน P การพิสูจน์. ให้ F เป็นมิติ n ส่วน P เห็นได้ชัดว่าทฤษฎีบทเป็นจริงถ้า n = 0 สมมติว่า n> 0 องค์ประกอบ n + 1 ใดๆ ของ F ขึ้นอยู่กับองค์ประกอบเชิงเส้นตรงของ P โดยเฉพาะอย่างยิ่ง ระบบขององค์ประกอบ 1, a, ..., an ขึ้นอยู่กับเชิงเส้น กล่าวคือ มีองค์ประกอบดังกล่าวใน P ที่มี 0, กับ 1, ... , cn ไม่เท่ากับศูนย์ทั้งหมด ดังนั้น c 0 × 1 + c 1 a +… + cnan = 0 ดังนั้น องค์ประกอบ a เป็นพีชคณิตมากกว่า P โปรดทราบว่ามีส่วนขยายเกี่ยวกับพีชคณิตของฟิลด์ที่ไม่ใช่ส่วนขยายที่จำกัด 2.2. การขยายสนามพีชคณิตแบบผสม ส่วนขยาย F ของฟิลด์ P เรียกว่า คอมโพสิต หากมี ห่วงโซ่จากน้อยไปหามากของฟิลด์ย่อย L i ของสนาม F เช่นนั้น P = L 0 - L 1 -… - L k = F และ k> 1 ทฤษฎีบท 2.3 ให้ F เป็นส่วนขยาย จำกัด ของ L และ L ส่วนขยาย จำกัด ของ P จากนั้น F คือส่วนขยาย จำกัด ของ P และ = @ [ล: ป]. การพิสูจน์. ปล่อยให้เป็น (1) a 1,…, a m เป็นฐานของสนาม L ส่วน P (เป็นเวคเตอร์สเปซ) และ (2) b 1,…, b n เป็นพื้นฐานของสนาม F ส่วน L องค์ประกอบใด ๆ d จาก F สามารถแสดงเป็นเส้นตรงในรูปของฐาน: (3) d = l 1 b 1 + ... + l n b n (l k 0L) สัมประสิทธิ์ 1 k สามารถแสดงเป็นเส้นตรงผ่านฐาน (1): (4) l k = p 1k a +… + p mk a m (p ik 0P) แทนที่นิพจน์สำหรับสัมประสิทธิ์ l k ใน (3) เราได้รับ d = е p ik a i b k. ดังนั้นแต่ละองค์ประกอบของสนาม F สามารถแสดงเป็นการรวมเชิงเส้นขององค์ประกอบของเซต B โดยที่ B = (a i b k1 (1, ..., m), k 0 (l, ..., n)) โปรดทราบว่าชุด B ประกอบด้วยองค์ประกอบนาโนเมตร ให้เราแสดงว่า B เป็นฐานของ F บนสนาม P เราต้องแสดงว่าระบบขององค์ประกอบของเซต B มีความเป็นอิสระเชิงเส้น ปล่อยให้เป็น (5) еc ik a i b k = 0, โดยที่ c ik 0 P. เนื่องจากระบบ (2) เป็นอิสระเชิงเส้นเหนือ L จึงตามมาจาก (5) นั้น (6) กับ 1 k a 1 + ... + กับ mk a m = 0 (k = 1, ..., n) เนื่องจากองค์ประกอบ a 1, ..., a m มีความเป็นอิสระเชิงเส้นตรงเหนือ P จึงตามมาจาก (6) นั้น ค 1 k = 0, ..., c mk = 0 (k = 1, ..., n), แสดงว่าสัมประสิทธิ์ทั้งหมดใน (5) มีค่าเท่ากับศูนย์ ดังนั้น ระบบขององค์ประกอบ B จึงเป็นอิสระเชิงเส้นและเป็นพื้นฐานของ F ส่วน P ดังนั้นจึงกำหนดได้ว่า = nm = × ดังนั้น F จึงเป็นส่วนขยายที่ จำกัด ของฟิลด์ P และสูตร (I) ถือเป็น คำนิยาม. ส่วนขยาย F ของฟิลด์ P เรียกว่า คอมโพสิทพีชคณิต ถ้ามีสายโซ่ย่อยของฟิลด์ P เพิ่มขึ้น P = L 0 - L 1 -… - L k = F และ k> 1 (1) เช่นนั้นสำหรับ i = 1, ..., k ฟิลด์ L i เป็นส่วนขยายเชิงพีชคณิตอย่างง่ายของฟิลด์ L i-1 หมายเลข k เรียกว่าความยาวของโซ่ (1) ข้อพิสูจน์ 2.4. ส่วนขยายพีชคณิตผสม F ของสนาม P คือส่วนขยายจำกัดของ P พิสูจน์ได้อย่างง่ายดายโดยการเหนี่ยวนำความยาวของโซ่ (1) ตามทฤษฎีบท 2.3 ทฤษฎีบท 2.5 ให้ 1, ..., k เป็นองค์ประกอบของสนาม F เกี่ยวกับพีชคณิตเหนือสนาม P จากนั้นฟิลด์ P (a 1, ..., a k) เป็นส่วนขยายที่แน่นอนของฟิลด์ P L 0 = P, L 1 = P, L 2 = P, ..., L k = P. จากนั้น L 1 = P เป็นส่วนขยายพีชคณิตอย่างง่ายของฟิลด์ L 0; L 2 เป็นการขยายพีชคณิตอย่างง่ายของสนาม L 1 ตั้งแต่ L 2 = P = (P) = L 1 = L 1 (a 2) เป็นต้น ดังนั้น, P = L 0 - L 1 -… - L k = F โดยที่ L i = L i -1 (a i) สำหรับ i = 1, ..., k นั่นคือสมาชิกแต่ละตัวของ chain (2) เป็นส่วนขยายพีชคณิตอย่างง่ายของสมาชิกก่อนหน้าของห่วงโซ่ ดังนั้น สนาม F จึงเป็นส่วนขยายเชิงพีชคณิตแบบประกอบของสนาม P ดังนั้นโดยอาศัยอำนาจตามข้อพิสูจน์ 2.4 สนาม F จึงเป็นส่วนขยายที่จำกัดของสนาม P ข้อพิสูจน์ 2.6. การขยายพีชคณิตแบบผสมของเขตข้อมูลหนึ่งคือส่วนขยายเกี่ยวกับพีชคณิตของเขตข้อมูลนี้ 2.3. ความเรียบง่ายของการขยายสนามพีชคณิตแบบผสม ทฤษฎีบท 2.7 ให้ฟิลด์ตัวเลข F เป็นส่วนขยายพีชคณิตประกอบของฟิลด์ P จากนั้น F คือส่วนขยายพีชคณิตอย่างง่ายของ P การพิสูจน์. ให้ P - L - F ยิ่งกว่านั้น L = P (a), F = L (b) และดังนั้น F = P (a, b) ให้ f และ g เป็นพหุนามน้อยที่สุดบน P สำหรับตัวเลข a และ b ตามลำดับ และ deg f = m, deg g = n พหุนาม f และ g จะลดทอนไม่ได้ในส่วน P ดังนั้นจึงไม่มีจำนวนเชิงซ้อนของรากหลายตัวในฟิลด์ E ปล่อยให้เป็น a = a 1, ..., a m คือรากของพหุนาม f ใน C และ b = b 1, ..., b n คือรากของพหุนาม g ใน C พิจารณาเซตจำกัด M: M = ((a i -a) / (b-b k) ½i0 (1,…, m), k0 (2,…, n)). เนื่องจาก P เป็นเซตตัวเลข (และด้วยเหตุนี้ จึงเป็นอนันต์) จึงมีตัวเลข c ใน P ที่แตกต่างจากองค์ประกอบของเซต M, c0P (M, cóM. Let แล้วความสัมพันธ์ (2) g ¹ a i + cb k = (i0 (1, ..., m), k0 (2, ..., n)) อันที่จริงในกรณีของความเท่าเทียมกัน a + cb = a i + cb k มันจะเป็น с = (a i -a) / (b-b k) 0 M ซึ่งจะขัดกับการเลือกหมายเลข c. ให้ F 1 = P (g) และ F 1 เป็นวงแหวนพหุนามใน x ให้ h = f (g - cx) เป็นพหุนามจาก F 1 [x] (g, c0P (g) = F 1) ให้เราแสดงให้เห็นว่า xb เป็นตัวหารร่วมมากของพหุนาม h และ g ในวงแหวน F 1 [x] เนื่องจาก g (b) = 0 ดังนั้น x-b จึงหาร g ใน E [x] นอกจากนี้ โดยอาศัยอำนาจตาม (1) ชั่วโมง (b) = f (g-cb) = f (a) = 0 ดังนั้น xb หารพหุนาม h ใน E [x] ดังนั้น x-b เป็นตัวหารร่วมของ h และ g ในวงแหวน E [x] ให้เราพิสูจน์ว่า g และ h ใน C ไม่มีรากอื่นนอกจาก b อันที่จริง สมมติว่า b k, k0 (2, ..., n) เป็นรูตร่วมของพวกมัน จากนั้น h (bk) = f (g - cb k) = 0 ดังนั้นจึงมีดัชนี i0 (1, ..., m) ซึ่ง g = ai + cb k (k> 1) ซึ่งขัดแย้งกัน (2 ). จากสิ่งนี้ เราสรุปได้ว่า xb เป็นตัวหารร่วมมากของ g และ h ใน E [x] เนื่องจาก x - b เป็นพหุนามนอร์มัลไลซ์ มันจึงตามมาว่า x - b เป็นตัวหารร่วมมากของ g และ h ในวงแหวน F 1 [x] ดังนั้น (x-b) 0 F 1 [x] และ b 0 F 1 = P (g) นอกจากนี้ a = g - cb 0 F 1 ดังนั้น, F = P (a, b) Ì F 1, F 1 ÌF 2.4. ช่องเลขพีชคณิต ในคลาสของฟิลด์ย่อยของฟิลด์ของจำนวนเชิงซ้อน หนึ่งในฟิลด์ที่สำคัญที่สุดคือฟิลด์ของตัวเลขเกี่ยวกับพีชคณิต คำนิยาม. จำนวนเชิงพีชคณิตคือจำนวนเชิงซ้อนที่เป็นรากของพหุนามที่มีดีกรีเป็นบวกพร้อมสัมประสิทธิ์ที่เป็นตรรกยะ โปรดทราบว่าจำนวนเชิงพีชคือจำนวนเชิงซ้อนใดๆ เกี่ยวกับพีชคณิตเหนือฟิลด์ Q โดยเฉพาะอย่างยิ่ง จำนวนตรรกยะใดๆ คือพีชคณิต ทฤษฎีบท 2.8 เซต A ของเลขพีชคณิตทั้งหมดปิดอยู่ในวงแหวน E = + С, +, -,, 1, จำนวนเชิงซ้อน พีชคณิต A = + A, +, -,, 1 เป็นฟิลด์ ซึ่งเป็นฟิลด์ย่อยของ E การพิสูจน์. ให้ a และ b เป็นองค์ประกอบใดๆ ของ A ตามข้อพิสูจน์ 2.6 สนาม Q (a, b) เป็นพีชคณิตมากกว่า Q ดังนั้นตัวเลข a + b, -а, ab, 1 เป็นพีชคณิต นั่นคือ มันเป็นของ เซต A ดังนั้น เซต A ถูกปิดภายใต้การดำเนินการหลักของวงแหวน E ดังนั้น พีชคณิต A ซึ่งเป็นวงแหวนย่อยของวงแหวน E จึงเป็นวงแหวน นอกจากนี้ ถ้า a เป็นองค์ประกอบที่ไม่ใช่ศูนย์ของ A ดังนั้น a -1 0 Q (a, b) ดังนั้น -1 จึงเป็นของ A ดังนั้น พีชคณิต A เป็นฟิลด์ ซึ่งเป็นฟิลด์ย่อยของ E คำนิยาม. ฟิลด์ A = + A, +, -,, 1 เรียกว่าฟิลด์ของตัวเลขพีชคณิต แสดงว่าจำนวน a = เป็นพีชคณิต วิธีการแก้. จาก a = ตาม a- ยกทั้งสองข้างของความเสมอภาคสุดท้ายยกกำลังสามกัน: 3 -3a 2 9a-3 = 2 3 + 9a-2 = 3 (a 2 +1) ตอนนี้เรายกความเสมอภาคทั้งสองข้างให้เป็นยกกำลังสอง: 6 + 18a 4 + 81a 2 -4a 3 -36a + 4 = 27a 4 + 54a 2 +27 6 -9a 4 -4a 3 + 27a 2 -36a-23 = 0 ดังนั้น a เป็นรากของพหุนาม f (x) = a 6 -9a 4 -4a 3 + 27a 2 -36a-23 = 0 ด้วยสัมประสิทธิ์ที่เป็นตรรกยะ ซึ่งหมายความว่า a เป็นจำนวนเชิงพีชคณิต 2.5. พีชคณิตปิดของฟิลด์ของตัวเลขพีชคณิต ทฤษฎีบท 2.9 ฟิลด์หมายเลขพีชคณิตถูกปิดเกี่ยวกับพีชคณิต การพิสูจน์. ให้ A [x] เป็นวงแหวนพหุนามใน x เหนือสนาม A ของจำนวนพีชคณิต ปล่อยให้เป็น f = a 0 + a 1 x + ... + a n x n (a 0, ..., a n 0 A) พหุนามใดๆ ของดีกรีบวกจาก A [x] เราต้องพิสูจน์ว่า f มีรากใน A เนื่องจาก f0C [x] และสนาม E ถูกปิดด้วยพีชคณิต f มีรากใน E นั่นคือ มีจำนวนเชิงซ้อน c อยู่ ดังนั้น f (c) = 0 ให้ L = Q (a 0, ..., a n) และ L (c) คือการขยายพีชคณิตอย่างง่ายของฟิลด์ L ด้วยความช่วยเหลือของ c จากนั้น Q - L - L (c) เป็นส่วนขยายพีชคณิตแบบจำกัดของสนาม L โดยทฤษฎีบท 2.2, L คือส่วนขยายแบบจำกัดของสนาม Q โดยทฤษฎีบท 2.3, L (c) เป็นส่วนขยายแบบจำกัดของสนาม Q ดังนั้น โดยทฤษฎีบท 2.2 จึงเป็นไปตามที่สนาม L (c) เป็นส่วนขยายเกี่ยวกับพีชคณิตของสนาม Q และด้วยเหตุนี้ c0A ดังนั้นพหุนามใดๆ จาก A [x] ของดีกรีบวกจะมีรากอยู่ใน A นั่นคือสนาม A ถูกปิดด้วยพีชคณิต 3. ส่วนขยายที่แยกออกได้และไม่สามารถแยกออกได้ ให้ D เป็นสนาม ให้เราหาว่าพหุนามที่แยกไม่ออกใน D [x] สามารถมีหลายรากได้หรือไม่? เพื่อให้ f (x) มีหลายราก พหุนาม f (x) และ fN (x) ต้องมีตัวประกอบร่วมอื่นที่ไม่ใช่ค่าคงที่ ซึ่งสามารถคำนวณได้อยู่แล้วใน D [x] หากพหุนาม f (x) แยกไม่ออก ดังนั้น f (x) จะไม่สามารถมีตัวประกอบร่วมที่ไม่คงที่กับพหุนามที่มีดีกรีน้อยกว่า ดังนั้น f "(x) = 0 จึงต้องมีความเท่าเทียมกัน ฉ (x) = 3a n x n fN (x) = 3na n x n -1 เนื่องจาก fN (x) = 0 แต่ละสัมประสิทธิ์จะต้องหายไป: na n = 0 (n = l, 2, ..., n) ในกรณีของศูนย์คุณลักษณะ นี่หมายความว่า a n = 0 สำหรับ n ¹ 0 ทั้งหมด ดังนั้น พหุนามที่ไม่คงที่จึงไม่สามารถมีหลายรากได้ ในกรณีของลักษณะเฉพาะ p ความเท่าเทียมกัน na n = 0 ก็เป็นไปได้เช่นกันสำหรับ n ¹ 0 แต่แล้วการเปรียบเทียบจะต้องสำเร็จ f (x) = a 0 + a p x p + a 2p x 2p +… ตรงกันข้าม: ถ้า f (x) มีรูปแบบนี้ ดังนั้น fN (x) = 0 ในกรณีนี้ เราสามารถเขียนว่า นี่เป็นการพิสูจน์คำยืนยัน: ในกรณีของศูนย์คุณลักษณะเฉพาะ พหุนาม f (x) ที่แยกไม่ออกใน D [x] มีรากง่าย ๆ เท่านั้น ในกรณีของ oce ที่มีลักษณะเฉพาะ p พหุนาม f (x) (ถ้าแตกต่างกัน จากค่าคงที่) มีหลายรากก็ต่อเมื่อสามารถแสดงเป็นพหุนาม j ใน xp ได้ ในกรณีหลังนี้ ปรากฎว่า j (x) เป็นพหุนามใน x p จากนั้น f (x) เป็นพหุนามใน x p 2 ให้ f (x) เป็นพหุนามใน x pe แต่ไม่ใช่พหุนามใน x pe +1 แน่นอน พหุนาม y (y) นั้นแยกไม่ออก นอกจากนี้ y ¢ (y) ¹ 0 เพราะไม่เช่นนั้น y (y) จะมีรูปแบบ c (yp) ดังนั้น f (x) จะถูกแสดงในรูปแบบ c (x pe + 1) ซึ่งขัดแย้งกับสมมติฐาน . ดังนั้น y (y) มีรากง่าย ๆ เท่านั้น เราขยายพหุนาม y (y) ในการขยายสนามภาคพื้นดินเป็นปัจจัยเชิงเส้น: m y (y) = J (y-b ผม). f (x) = J (x pe -b ผม) ให้ a i เป็นรากของพหุนาม x pe -b i จากนั้น x i pe = b i, x pe -b i = x pe - ai pe = (x-a i) pe ดังนั้น a i เป็นรากของพหุนามหลายตัวของพหุนาม x pe -b i และ f (x) = J (x -a i) p e. รากทั้งหมดของพหุนาม f (x) จึงมีหลายหลาก p e เท่ากัน ดีกรี m ของพหุนาม y เรียกว่า ดีกรีที่ลดลงของพหุนาม f (x) (หรือรูต a i); จำนวน e เรียกว่าเลขชี้กำลังของพหุนาม f (x) (หรือของราก a i) เหนือสนาม D ระหว่างดีกรี ดีกรีที่ลดลงและเลขชี้กำลัง ความสัมพันธ์ โดยที่ m เท่ากับจำนวนรากที่แตกต่างกันของพหุนาม f (x) ถ้า q เป็นรูทของพหุนามที่แยกไม่ออกในวงแหวน D [x] และมีเพียงรูตธรรมดาเท่านั้น ดังนั้น q จะถูกเรียกว่าองค์ประกอบที่แยกออกได้บน D หรือองค์ประกอบประเภทที่หนึ่งส่วน D 1) ยิ่งกว่านั้น พหุนามที่แยกไม่ออกซึ่งรากทั้งหมดสามารถแยกออกได้นั้นเรียกว่าแยกออกได้ มิฉะนั้น องค์ประกอบพีชคณิต q และพหุนามที่แยกไม่ออก f (x) จะเรียกว่าแยกออกไม่ได้หรือองค์ประกอบ (ตามลำดับ พหุนาม) ชนิดที่สอง สุดท้าย ส่วนขยายเกี่ยวกับพีชคณิต S ซึ่งองค์ประกอบทั้งหมดแยกออกจาก D ได้ เรียกว่าแยกออกได้ส่วน D และส่วนขยายพีชคณิตอื่นๆ เรียกว่าแยกออกไม่ได้ ในกรณีของศูนย์คุณลักษณะ ตามสิ่งที่กล่าวไว้ข้างต้น พหุนามที่แยกไม่ออกทุกอัน (และด้วยเหตุนี้ทุกส่วนขยายเกี่ยวกับพีชคณิต) จะถูกแยกออกได้ เราจะเห็นในภายหลังว่าส่วนขยายฟิลด์ที่สำคัญและน่าสนใจส่วนใหญ่สามารถแยกออกได้ และมีคลาสของฟิลด์ทั้งหมดที่ไม่มีส่วนขยายที่แยกออกไม่ได้เลย (เรียกว่า "ฟิลด์ที่สมบูรณ์แบบ") ด้วยเหตุผลนี้ ในอนาคต ทุกอย่างที่เกี่ยวข้องกับส่วนขยายที่แยกออกไม่ได้โดยเฉพาะจะถูกพิมพ์เป็นตัวพิมพ์เล็ก พิจารณาตอนนี้ส่วนขยายเกี่ยวกับพีชคณิต S = D (q) เมื่อดีกรี n ของสมการ f (x) = 0 ที่กำหนดส่วนขยายนี้เท่ากับดีกรี (S: D) ดีกรีที่ลดลง m จะเท่ากับจำนวน isomorphisms ของสนาม S ในแง่ต่อไปนี้: พิจารณาเฉพาะ isomorphisms S @ S "ซึ่งองค์ประกอบของช่องย่อย D ยังคงคงที่และดังนั้น S จึงถูกแปลเป็นฟิลด์ที่เทียบเท่า S "( isomorphisms ของฟิลด์ S เหนือฟิลด์ D) และที่ฟิลด์รูปภาพ S" ร่วมกับสนาม S ภายในสนามทั่วไป W ภายใต้เงื่อนไขเหล่านี้ ทฤษฎีบทต่อไปนี้ถือเป็น: สำหรับตัวเลือกที่เหมาะสมของฟิลด์ W ส่วนขยาย S = D (q) มี m isomorphisms มากกว่า D และสำหรับตัวเลือกใดๆ ของฟิลด์ W ฟิลด์ S จะต้องไม่เกิน m isomorphisms ดังกล่าว การพิสูจน์. มอร์ฟฟิซึมเหนือ D แต่ละรายการจะต้องแมปองค์ประกอบ q กับองค์ประกอบคอนจูเกต q "จาก W เลือก W เพื่อให้ f (x) สลายตัวเหนือ W เป็นตัวประกอบเชิงเส้น จากนั้นปรากฎว่าองค์ประกอบ q มีองค์ประกอบคอนจูเกต m พอดี q, q" , ... ในกรณีนี้ ไม่ว่าจะเลือกฟิลด์ W อย่างไร องค์ประกอบ q จะมีคอนจูเกตไม่เกิน m ในนั้น โปรดทราบว่าตอนนี้ทุก isomorphism D (q) @D (q ") บน D ถูกกำหนดโดยสมบูรณ์โดยการระบุการติดต่อ q®q" แท้จริงแล้วถ้า q ไปที่ q "และองค์ประกอบทั้งหมดของ D ยังคงอยู่ในตำแหน่งดังนั้นองค์ประกอบ 3a k q k (ก 0D) ควรไป และสิ่งนี้กำหนด isomorphism โดยเฉพาะอย่างยิ่ง ถ้า q เป็นองค์ประกอบที่แยกออกได้ ดังนั้น m = n ดังนั้น จำนวนของ isomorphisms เหนือสนามภาคพื้นดินจะเท่ากับระดับของการขยาย หากมีฟิลด์คงที่บางฟิลด์ที่มีฟิลด์ที่พิจารณาทั้งหมด ซึ่งมีรูททั้งหมดของแต่ละสมการ f (x) = 0 (เช่น ในฟิลด์ของจำนวนเชิงซ้อน) ดังนั้นใน W เราสามารถใช้ฟิลด์นี้ได้เพียงครั้งเดียวและ สำหรับทุกคนแล้วจึงยกเลิกการเพิ่ม "ภายใน W บางส่วน" ในทุกคำสั่งของ isomorphism สิ่งนี้ทำเสมอในทฤษฎีสนามจำนวน เราจะเห็นในภายหลังว่าสำหรับฟิลด์นามธรรม สามารถสร้างฟิลด์ W. ทฤษฎีบทข้างต้นถูกทำให้เป็นแบบทั่วไปโดยข้อความต่อไปนี้: ถ้าส่วนขยาย S ได้มาจาก D โดยการเพิ่ม m . อย่างต่อเนื่อง องค์ประกอบพีชคณิต a 1, ..., a m และแต่ละ i - เป็นรูต ย่อยสลายไม่ได้เหนือสมการ D (a 1, ..., a i-1) ของดีกรีที่ลดลง n "i แล้ว นามสกุล S มี isomorphisms Õn i ¢ ตรงเหนือ D และไม่มีใน ส่วนขยายไม่มี isomorphisms ดังกล่าวของสนาม S อีกต่อไป การพิสูจน์. สำหรับ m = 1 ทฤษฎีบทได้รับการพิสูจน์แล้วข้างต้น สมมติว่าใช้ได้กับส่วนขยาย S 1 = D (a 1, ..., a m-1): ในส่วนขยายที่เหมาะสมบางส่วน W 1 คือ Õ n i ¢ isomorphisms ของสนาม S ส่วน D ให้ S 1 ®S 1 เป็นหนึ่งในไอโซมอร์ฟิซึมของ Õ n i ¢ เหล่านี้ มันถูกยืนยันว่าในฟิลด์ที่เลือกอย่างเหมาะสม W มันสามารถขยายเป็น isomorphism S = S 1 (a m) @ S = S (a m) ได้มากสุด n ¢ m วิธี องค์ประกอบ a m เป็นไปตามสมการ f 1 (x) = 0 ส่วน S 1 โดยมีรากต่างกัน n ¢ m การใช้ isomorphism S 1 ® S 1 ทำให้พหุนาม f 1 (x) กลายเป็นพหุนาม f 1 (x) แต่แล้ว f 1 (x) ในส่วนขยายที่เหมาะสมจะมีรากที่แตกต่างกันอีกครั้ง n ¢ m และอย่างมากที่สุด ให้ m เป็นหนึ่งในรากเหล่านี้ โดยการเลือกองค์ประกอบ a m ค่า isomorphism S 1 @ S 1 สามารถขยายไปยัง isomorphism S (a m) @ S (a m) ด้วย a m ®a m ได้ทางเดียวเท่านั้น: แน่นอน ความต่อเนื่องนี้ถูกกำหนดโดยสูตร еc k a m k ®å c k a m k เนื่องจากการเลือกองค์ประกอบ a m สามารถทำได้ใน n "m วิธี มีส่วนขยาย n" m ประเภทนี้สำหรับ isomorphism ที่เลือก е 1 ® е 1 เนื่องจากสามารถเลือก isomorphism นี้ได้ Õ n "ฉันทาง แล้วทุกอย่างก็มีอยู่ (ในฟิลด์ W ซึ่งมีรากทั้งหมดของสมการทั้งหมดที่อยู่ระหว่างการพิจารณา) Õ n "i × n" m = Õ n "i ของ isomorphisms ของส่วนขยาย S บนสนาม D ตามต้องการ ถ้า ni คือดีกรีเต็ม (ไม่ลด) ขององค์ประกอบ ai ส่วน D (a 1, ..., a i-1) ดังนั้น ni จะเท่ากับดีกรีของส่วนขยาย D (a 1, ..., ai) ของสนาม D (a 1, .. ., a i-1); ดังนั้น ดีกรี (S:D) คือ ถ้าเราเปรียบเทียบตัวเลขนี้กับจำนวน isomorphisms จำนวน isomorphisms ของส่วนขยาย S = D (a 1, ..., am) บน D (ในส่วนขยายที่เหมาะสมบางอย่าง W) เท่ากับดีกรี (S: D) หากแต่ละองค์ประกอบ ai แยกออกจากฟิลด์ได้ D (a 1,. .., a i-1). หากองค์ประกอบ a i อย่างน้อยหนึ่งตัวแยกกันไม่ได้ในฟิลด์ที่เกี่ยวข้อง จำนวน isomorphisms จะน้อยกว่าระดับของการขยาย ผลที่สำคัญหลายประการตามมาจากทฤษฎีบทนี้ทันที ประการแรก ทฤษฎีบทยืนยันว่าคุณสมบัติของแต่ละองค์ประกอบ a i ที่จะแยกจากฟิลด์ก่อนหน้านั้นเป็นคุณสมบัติของส่วนขยาย S เอง โดยไม่คำนึงถึงตัวเลือกขององค์ประกอบที่สร้าง a i เนื่องจากองค์ประกอบที่กำหนดเอง b ของสนามสามารถใช้เป็นเครื่องกำเนิดแรกได้ องค์ประกอบ b จึงกลายเป็นว่าแยกออกได้หาก a i ทั้งหมดแยกออกได้ ดังนั้น: ถ้าองค์ประกอบ ai, ..., an ถูกเชื่อมเข้ากับฟิลด์ D ตามลำดับ และแต่ละองค์ประกอบ ai นั้นสามารถแยกออกจากฟิลด์ที่ได้รับโดยการรวมองค์ประกอบก่อนหน้า a 1, a 2, ..., a i-1, แล้วนามสกุล S = D (a 1, ..., a n) แยกส่วนได้ส่วน D โดยเฉพาะอย่างยิ่ง ผลรวม ความแตกต่าง ผลิตภัณฑ์ และความฉลาดขององค์ประกอบที่แยกออกได้นั้นสามารถแยกออกได้ นอกจากนี้ หาก b แยกออกได้ในส่วน S และสนาม S แยกส่วนได้เหนือ D แล้ว องค์ประกอบ b ก็สามารถแยกออกได้ในส่วน D ซึ่งอธิบายได้จากข้อเท็จจริงที่ว่า b เป็นไปตามสมการบางตัวที่มีสัมประสิทธิ์จำนวนจำกัด a 1, ... , am จาก S และสามารถแยกออกได้บน D (a 1, ..., am) ดังนั้น ส่วนขยาย D (a 1, ..., a m, b). สุดท้าย ข้อเสนอต่อไปนี้ถือ: จำนวนของ isomorphisms ของส่วนขยายที่แยกออกได้แบบจำกัด S บนสนาม D เท่ากับระดับของส่วนขยาย (S: D) 4. การขยายฟิลด์ที่ไม่มีที่สิ้นสุด แต่ละฟิลด์ได้มาจากฟิลด์ย่อยอย่างง่ายโดยใช้ส่วนขยายแบบจำกัดหรือแบบอนันต์ บทนี้เกี่ยวข้องกับส่วนขยายฟิลด์อนันต์ พีชคณิตแรก และเหนือธรรมชาติ 4.1. เขตข้อมูลพีชคณิตปิด ในบรรดาส่วนขยายเกี่ยวกับพีชคณิตของเขตข้อมูลที่กำหนด บทบาทที่สำคัญคือ เล่นโดยส่วนขยายเกี่ยวกับพีชคณิตสูงสุด นั่นคือส่วนที่ไม่ยอมรับส่วนขยายเกี่ยวกับพีชคณิตเพิ่มเติม การมีอยู่ของส่วนขยายดังกล่าวจะได้รับการพิสูจน์ในส่วนนี้ เพื่อให้สนาม W เป็นการขยายพีชคณิตสูงสุด จำเป็นต้องมีเงื่อนไขต่อไปนี้: พหุนามแต่ละพหุนามของวงแหวน W [x] สามารถย่อยสลายเป็นปัจจัยเชิงเส้นได้อย่างสมบูรณ์ เงื่อนไขนี้ก็เพียงพอแล้ว ที่จริงแล้ว หากพหุนามทั้งหมดใน W [x] สามารถแยกออกเป็นปัจจัยเชิงเส้นได้ ดังนั้นพหุนามอย่างง่ายทั้งหมดใน W [x] จะเป็นเส้นตรง และทุกองค์ประกอบของส่วนขยายพีชคณิต W "ของสนาม W จะกลายเป็นรากของเส้นตรงบางตัว พหุนาม x - a ใน W [x] นั่นคือมันตรงกับองค์ประกอบ a ของ W ดังนั้นเราจึงให้คำจำกัดความต่อไปนี้: สนาม W ถูกเรียกว่าปิดเชิงพีชคณิต ถ้าพหุนามใดๆ ใน W [x] สามารถแตกตัวเป็นปัจจัยเชิงเส้นได้ คำจำกัดความที่เทียบเท่ากันมีดังต่อไปนี้: สนาม W ถูกปิดเชิงพีชคณิต ถ้าพหุนามทุกพหุนามจาก W [x] ที่แตกต่างจากค่าคงที่มีอย่างน้อยหนึ่งรูตใน W นั่นคือ ปัจจัยเชิงเส้นอย่างน้อยหนึ่งตัวใน W [x] อันที่จริง หากเงื่อนไขดังกล่าวเป็นที่น่าพอใจและพหุนาม f (x) โดยอำเภอใจถูกแยกย่อยเป็นปัจจัยที่แยกไม่ออก พวกมันทั้งหมดจะต้องเป็นเส้นตรง "ทฤษฎีบทพื้นฐานของพีชคณิต" ระบุว่าสนามของจำนวนเชิงซ้อนถูกปิดด้วยพีชคณิต ตัวอย่างต่อไปของฟิลด์ปิดเชิงพีชคณิตคือฟิลด์ของจำนวนเชิงซ้อนเชิงพีชคณิตทั้งหมด นั่นคือ ชุดของจำนวนเชิงซ้อนเหล่านั้นที่ตรงตามสมการบางตัวที่มีสัมประสิทธิ์ที่เป็นตรรกยะ รากที่ซับซ้อนของสมการที่มีสัมประสิทธิ์เกี่ยวกับพีชคณิตนั้นไม่ใช่เฉพาะด้านพีชคณิตเท่านั้น แต่ยังครอบคลุมสนามของจำนวนตรรกยะด้วย นั่นคือ พวกมันเองเป็นตัวเลขเกี่ยวกับพีชคณิต ที่นี่เราจะแสดงวิธีสร้างส่วนขยายแบบปิดเชิงพีชคณิตของฟิลด์ P ที่กำหนดโดยพลการ และยิ่งไปกว่านั้น ในทางพีชคณิตล้วนๆ Steinitz อยู่ในกลุ่มต่อไปนี้ ทฤษฎีบทหลัก สำหรับแต่ละฟิลด์ P มีส่วนขยายเกี่ยวกับพีชคณิตแบบปิดเกี่ยวกับพีชคณิต W อยู่ ส่วนขยายนี้ถูกกำหนดไว้อย่างไม่ซ้ำกันจนถึงความเท่าเทียมกัน: ส่วนขยายพีชคณิตที่ปิดด้วยพีชคณิตสองส่วน W, W "ของฟิลด์ P มีค่าเท่ากัน เราต้องนำการพิสูจน์ทฤษฎีบทนี้ด้วยบทแทรกหลายข้อ: บทแทรก 1. ให้ W เป็นส่วนขยายเกี่ยวกับพีชคณิตของสนาม P เงื่อนไขที่เพียงพอสำหรับ W ที่จะปิดพีชคณิตคือการแยกตัวประกอบของพหุนามใดๆ จาก P [x] ในวงแหวน W [x] การพิสูจน์. ให้ f (x) เป็นพหุนามตามอำเภอใจจาก W [x] หากมันไม่สลายตัวเป็นปัจจัยเชิงเส้น เราก็สามารถเพิ่มรูท a ของมันและได้โอเวอร์ฟิลด์ W " องค์ประกอบ a เป็นพีชคณิตมากกว่า W และ W คือส่วนขยายเกี่ยวกับพีชคณิตของฟิลด์ P ดังนั้น องค์ประกอบ a เป็นพีชคณิตเหนือ P ดังนั้น รากของพหุนามบางตัว g (x) จาก P [x] พหุนามนี้ถูกแยกย่อยใน W [x] เป็นตัวประกอบเชิงเส้น ดังนั้น -root ของตัวประกอบเชิงเส้นบางตัวใน W [x] นั่นคือเป็นของฟิลด์ W ซึ่งขัดแย้งกับสมมติฐาน ... เล็มมา 2 หากฟิลด์ P มีการจัดลำดับอย่างดี วงแหวนของพหุนาม P [x] ก็สามารถจัดลำดับได้อย่างดี และยิ่งกว่านั้น ในการจัดลำดับฟิลด์ P จะเป็นเซ็กเมนต์ การพิสูจน์. เรากำหนดความสัมพันธ์ของลำดับระหว่างพหุนาม f (x) จาก P [x] ดังนี้: ให้ f (x) 1) ระดับของ f (x) น้อยกว่าระดับของ g (x); 2) ดีกรีของ f (x) เท่ากับดีกรีของ g (x) และเท่ากับ n นั่นคือ f (x) = a 0 x n + ... + a n, g (x) = b 0 x n + ... + b n และสำหรับดัชนีบางตัว k: และ i = b ฉัน สำหรับ i ก ในกรณีนี้มีข้อยกเว้นสำหรับพหุนาม 0: ดีกรี 0 ถูกกำหนด เห็นได้ชัดว่าด้วยวิธีนี้เราได้รับคำสั่งบางอย่างในแง่ที่ P [x] ได้รับคำสั่งอย่างสมบูรณ์ แสดงดังนี้: ในทุกชุดของพหุนามที่ไม่ว่างเปล่าจะมีชุดย่อยที่ไม่ว่างของพหุนามดีกรีน้อยที่สุด ปล่อยให้มันเท่ากับ n เซตย่อยนี้ประกอบด้วยเซตย่อยของพหุนามที่ไม่ว่างเปล่า ค่าสัมประสิทธิ์ a 0 ซึ่งเป็นค่าแรกในความหมายของลำดับที่มีอยู่ท่ามกลางเงื่อนไขอิสระของพหุนามที่กำลังพิจารณา ในชุดย่อยนี้มีชุดย่อยของพหุนามที่มี 1 ตัวแรก ฯลฯ เซตย่อยที่มี a ตัวแรกซึ่งในท้ายที่สุดจะกลายเป็นพหุนามเดียว (ตั้งแต่ 0, .. ., และ n ถูกกำหนดไว้อย่างชัดเจนเนื่องจากเงื่อนไขขั้นต่ำที่เติมเต็มอย่างสม่ำเสมอในตัวเลือก); พหุนามนี้เป็นองค์ประกอบแรกในชุด เล็มมา 3 หากฟิลด์ P มีลำดับที่ดีและพหุนาม f (x) ขององศา n และ n สัญลักษณ์ a 1 ... an จะได้รับ จากนั้นฟิลด์ P (a 1, ..., an) ซึ่ง f (x) ถูกย่อยสลายอย่างสมบูรณ์เป็นปัจจัยเชิงเส้น Õ (x-a i) ถูกสร้างขึ้นอย่างมีเอกลักษณ์และสมบูรณ์ เป็นระเบียบ ฟิลด์ P ในแง่ของลำดับนี้คือเซ็กเมนต์ การพิสูจน์. เราจะแนบราก a 1 ..., a n ตามลำดับซึ่งเป็นผลมาจากการที่ฟิลด์ P 1, ..., P n จะปรากฏขึ้นตามลำดับจาก P = P 0 สมมติว่า P i-1 = P (a 1 ..., a i-1) เป็นฟิลด์ที่สร้างไว้แล้วและ P เป็นส่วนใน P i-1; จากนั้น Р i จะถูกสร้างขึ้นดังนี้ ประการแรก โดยอาศัยอำนาจตามเล็มมา 2 วงแหวนพหุนาม P i-1 [x] ได้รับการจัดลำดับอย่างสมบูรณ์ พหุนาม f ถูกย่อยสลายในวงแหวนนี้เป็นปัจจัยที่แยกไม่ออก โดยที่แรกจะเป็น x - a 1, ..., x - a i-1; ในบรรดาปัจจัยที่เหลือ ให้ f i (x) เป็นลำดับแรกในความหมายของลำดับที่มีอยู่ ร่วมกับสัญลักษณ์ a i หมายถึงรูทของพหุนาม f i (x) เรากำหนดฟิลด์ Р i = P i -1 เป็นการรวบรวมผลรวมทั้งหมด โดยที่ h คือดีกรีของพหุนาม f i (x) ถ้า f i (x) เป็นเส้นตรง แน่นอนว่าเราตั้งค่า P i = P i -1; ในกรณีนี้ไม่จำเป็นต้องใช้สัญลักษณ์ a i ฟิลด์ที่สร้างถูกเรียงลำดับอย่างสมบูรณ์โดยใช้เงื่อนไขต่อไปนี้: แต่ละองค์ประกอบของฟิลด์ เปรียบเทียบพหุนาม และองค์ประกอบของสนามได้รับการจัดลำดับในลักษณะเดียวกับการเรียงลำดับพหุนามที่สอดคล้องกัน เห็นได้ชัดว่า P i-1 คือเซ็กเมนต์ใน Pi ดังนั้น P คือเซ็กเมนต์ใน P i ดังนั้นฟิลด์ Р 1, ..., Р n จึงถูกสร้างขึ้นและได้รับการสั่งซื้ออย่างสมบูรณ์ ฟิลด์ Р n คือฟิลด์ P ที่กำหนดอย่างเฉพาะเจาะจงที่จำเป็น (a 1, ..., a n) เล็มมา 4 หากอยู่ในชุดของฟิลด์ที่เรียงลำดับ แต่ละฟิลด์ก่อนหน้าเป็นฟิลด์ย่อยของฟิลด์ถัดไป การรวมของฟิลด์เหล่านี้คือฟิลด์ การพิสูจน์. สำหรับสององค์ประกอบ a, b ของยูเนี่ยน มีสองฟิลด์ S a, S b ซึ่งมี a และ b และฟิลด์หนึ่งนำหน้าอีกฟิลด์หนึ่ง ในฟิลด์ที่ล้อมรอบ มีการกำหนดองค์ประกอบ a + b และ a × b และนี่คือวิธีการกำหนดองค์ประกอบเหล่านี้ในแต่ละฟิลด์ที่มี a และ b เนื่องจากสองฟิลด์ดังกล่าว ฟิลด์หนึ่งอยู่ก่อนอีกฟิลด์หนึ่งและเป็นฟิลด์ย่อย . ตัวอย่างเช่น เพื่อพิสูจน์กฎแห่งการเชื่อมโยง ab g = bg, ค้นหาระหว่างฟิลด์ S a, Sb, S g ที่มีสองฟิลด์อื่น (ที่ใหญ่ที่สุด); ฟิลด์นี้มี a, b และ g และกฎการเชื่อมโยงเป็นที่พอใจ กฎการคำนวณอื่นๆ ทั้งหมดที่มีองค์ประกอบยูเนียนจะได้รับการตรวจสอบในลักษณะเดียวกัน การพิสูจน์ทฤษฎีบทหลักแบ่งออกเป็นสองส่วน: การสร้างสนาม W และการพิสูจน์เอกลักษณ์ การสร้างสนาม W .. เล็มมา 1 บ่งชี้ว่าในการสร้างส่วนขยายปิดเชิงพีชคณิต W ของสนาม P ก็เพียงพอแล้วที่จะสร้างส่วนขยายเกี่ยวกับพีชคณิตของสนาม P โดยที่แต่ละพหุนามจาก P [x] จะสลายตัวเหนือส่วนขยายนี้เป็นเส้นตรง ปัจจัย. 1. ฟิลด์ Р f คือยูเนียนของฟิลด์ Р และทุกฟิลด์ S g สำหรับ g 2. ฟิลด์ Р f ได้รับคำสั่งอย่างสมบูรณ์เพื่อให้ Р และทุกฟิลด์ S g สำหรับ g 3. ฟิลด์ S f ได้มาจาก Р f โดยการเพิ่มรากทั้งหมดของพหุนาม f โดยใช้สัญลักษณ์ a 1, ..., a n ตาม Lemma 3 จำเป็นต้องพิสูจน์ว่าด้วยวิธีนี้ฟิลด์ที่ได้รับคำสั่งอย่างดี Р f, S f ถูกกำหนดอย่างเฉพาะเจาะจงจริงๆ ถ้าเฉพาะ Р g, S g ก่อนหน้าทั้งหมดถูกกำหนดไว้แล้วโดยข้อกำหนดที่ระบุไว้ข้างต้น หากเป็นไปตามข้อกำหนด 3 อันดับแรก Р f คือเซ็กเมนต์ใน S f จากนี้ไปและข้อกำหนด 2 ว่าฟิลด์ P และแต่ละฟิลด์ S g (g Р - ส่วนใน S h ที่ h S g - ส่วนใน S h ที่ g ดังนั้นจึงเป็นไปตามที่สนาม P และสนาม S h (h ตามเงื่อนไขที่ 3 พหุนาม f (x) จะถูกย่อยสลายอย่างสมบูรณ์เป็นปัจจัยเชิงเส้นในสนาม S f นอกจากนี้ โดยใช้การเหนี่ยวนำแบบทรานส์ไฟไนต์ แสดงว่า S f เป็นพีชคณิตเหนือ P ที่จริงแล้ว สมมติว่าเขตข้อมูลทั้งหมด S g (g ตอนนี้ให้เราเขียนสหภาพ W ของทุกสาขา S f; ตามเล็มมา 4 มันคือทุ่งนา ฟิลด์นี้เป็นพีชคณิตบน P และพหุนามทั้งหมด f สลายตัวทับมัน (เนื่องจากพหุนามทุกอัน f ถูกสลายไปแล้วในส่วน S f) ดังนั้น ฟิลด์ W ถูกปิดเชิงพีชคณิต (บทที่ 1) เอกลักษณ์ของสนาม ว. ให้ W และ W "เป็นสองฟิลด์ที่เป็นพีชคณิตและพีชคณิตปิดส่วนขยายของฟิลด์ P. เราพิสูจน์ความเท่าเทียมกันของฟิลด์เหล่านี้. ด้วยเหตุนี้ เราถือว่าทั้งสองฟิลด์ได้รับการเรียงลำดับอย่างสมบูรณ์ สำหรับแต่ละฟิลด์ เซ็กเมนต์ J จาก W (ฟิลด์ W เองก็ถือว่าเป็นหนึ่งในเซ็กเมนต์ดังกล่าว) เซตย่อย J ¢ใน W "และ isomorphism บางส่วน พี (Â) @ พี ( ¢). หลังต้องตอบสนองความสัมพันธ์ที่เกิดซ้ำดังต่อไปนี้ 1. isomorphism P (Â) @ P ( ¢) ต้องปล่อยให้แต่ละองค์ประกอบของฟิลด์ P อยู่กับที่ 2. isomorphism P (J) @ P (J,) สำหรับ ÁÌ J ต้องเป็นส่วนขยายของ isomorphism P () @ P (") 3. หาก J มีองค์ประกอบสุดท้าย a ดังนั้น J = ÁÈ (a) และหาก a เป็นรากของพหุนาม f (x) ที่แยกไม่ออกใน P () ดังนั้นองค์ประกอบ a "จะต้องเป็นรากแรกของ สอดคล้องโดยอาศัยอำนาจตาม P () @ Р (Á "), พหุนาม f ¢ (x) ในช่องที่มีการจัดลำดับอย่างดี W" จำเป็นต้องแสดงให้เห็นว่าข้อกำหนดทั้งสามนี้กำหนด isomorphism P (J) @ P (J,) จริงๆ หากกำหนดไว้แล้วสำหรับกลุ่มก่อนหน้าทั้งหมด ÁÌ J ต้องแยกเป็นสองกรณีที่นี่ กรณีแรก. ชุดไม่มีองค์ประกอบสุดท้าย จากนั้นแต่ละองค์ประกอบ a เป็นของส่วนก่อนหน้า Á; ดังนั้น J คือการรวมกันของส่วน Á ดังนั้น P (J) จึงเป็นการรวมของเขตข้อมูล P () สำหรับ ÁÌ J เนื่องจากแต่ละ isomorphisms P (Á) @ P (Á ") คือความต่อเนื่องขององค์ประกอบก่อนหน้าทั้งหมด แต่ละองค์ประกอบ a สำหรับ isomorphisms เหล่านี้ทั้งหมดมีความเกี่ยวข้องกับองค์ประกอบ a เพียงตัวเดียว" ดังนั้นจึงมีการแมป P (J) → P (J) เพียงหนึ่งรายการเท่านั้น ซึ่งจะดำเนินต่อจาก isomorphisms ก่อนหน้าทั้งหมด P () → P (") คือ -map a®a" เห็นได้ชัดว่ามันเป็น isomorphism และเป็นไปตามข้อกำหนด 1 และ 2 กรณีที่สอง ชุด  มีองค์ประกอบสุดท้าย a; ดังนั้น  = ÁÈ (ก) เนื่องจากข้อกำหนด 3 องค์ประกอบ a " ซึ่งสัมพันธ์กับองค์ประกอบ a จึงถูกกำหนดอย่างเฉพาะเจาะจง เนื่องจาก a" อยู่เหนือฟิลด์ P (") (ในความหมายของ isomorphism ที่พิจารณา) จึงเป็นไปตาม" สมการที่แยกไม่ออกได้เหมือนกับ a เหนือ P (Á) ตามด้วย isomorphism P (Á) → P (") (และในกรณีที่ว่างเปล่า นั่นคือ เอกลักษณ์ของอัตลักษณ์ P®P) ขยายไปถึง isomorphism P (Á, a) ®P ( ", a ¢) สำหรับตำแหน่งที่ a เข้าสู่ a ". isomorphism นี้ถูกกำหนดโดยข้อกำหนดข้างต้นโดยเฉพาะ เนื่องจากแต่ละฟังก์ชันตรรกยะ j (a) ที่มีค่าสัมประสิทธิ์จาก J จะต้องไปที่ฟังก์ชัน j "(a") ด้วยสัมประสิทธิ์ที่สอดคล้องกันจาก Á " ไอโซมอร์ฟิซึม P (J) ® Р (Â) เป็นไปตามข้อกำหนด 1 และ 2 อย่างเห็นได้ชัด เสร็จสิ้นการสร้าง isomorphism P (J) → P (J) เราแสดงโดย W "การรวมกันของทุกฟิลด์ P (J) จากนั้นมี isomorphism P (W) ®W" หรือ W®W " ซึ่งทำให้แต่ละองค์ประกอบของสนาม P. เนื่องจากสนาม W เป็นพีชคณิต ปิด ดังนั้นต้องเป็น W " ดังนั้น W" จึงเกิดขึ้นพร้อมกับฟิลด์ W ทั้งหมด ดังนั้น ความเท่าเทียมกันของฟิลด์ W และ W ¢ ความหมายของการขยายแบบปิดเชิงพีชคณิตของเขตข้อมูลที่กำหนดคือ จนถึงความเท่าเทียมกัน มีส่วนขยายเกี่ยวกับพีชคณิตที่เป็นไปได้ทั้งหมดของเขตข้อมูลนี้ อย่างแม่นยำมากขึ้น: ถ้า W คือส่วนขยายเกี่ยวกับพีชคณิตแบบปิดเชิงพีชคณิตของเขตข้อมูล P และ S คือส่วนขยายพีชคณิตที่กำหนดเองของเขตข้อมูล P ดังนั้นภายใน W จะมีส่วนขยาย S 0 ที่เทียบเท่ากับ S การพิสูจน์. เราขยาย S เป็นส่วนขยายพีชคณิตแบบปิดบางส่วน W " นอกจากนี้ยังจะเป็นพีชคณิตมากกว่า P และดังนั้นจึงเทียบเท่ากับส่วนขยาย W สำหรับ isomorphism บางอย่างที่นำ W ไปเป็น W และทำให้แต่ละองค์ประกอบของ P คงที่ ช่อง S จะเข้าสู่บางส่วน ฟิลด์ย่อยที่เทียบเท่า S 0 ใน W 4.2. ส่วนขยายที่ยอดเยี่ยมอย่างง่าย ส่วนขยายเหนือธรรมชาติอย่างง่ายแต่ละอันของสนาม D ดังที่เราทราบ เทียบเท่ากับสนามของผลหาร D (x) ของวงแหวนพหุนาม D [x] ดังนั้นเราจะศึกษาด้านนี้ของผลหาร องค์ประกอบของสนาม W เป็นฟังก์ชันที่มีเหตุผล ทฤษฎีบท. ทุกองค์ประกอบ h ของดีกรี n ที่แตกต่างจากค่าคงที่นั้นอยู่เหนือ D และสนาม D (x) เป็นส่วนขยายเกี่ยวกับพีชคณิตของฟิลด์ D (h) ของดีกรี n การพิสูจน์. การแทนค่า h = f (x) / g (x) จะถือว่าลดไม่ได้ จากนั้นองค์ประกอบ x เป็นไปตามสมการ g (x) × h - f (x) = 0 โดยมีค่าสัมประสิทธิ์จาก D (h) สัมประสิทธิ์เหล่านี้ไม่สามารถเป็นศูนย์ได้ทั้งหมด อันที่จริง หากพวกมันทั้งหมดมีค่าเท่ากับศูนย์ และ a จะเป็นสัมประสิทธิ์ที่ไม่ใช่ศูนย์ของพหุนาม g (x) สำหรับดีกรี x เดียวกัน และ b k จะเป็นสัมประสิทธิ์ที่ไม่เป็นศูนย์ของพหุนาม f (x) แล้ว ความเท่าเทียมกัน โดยที่ h = b k / a k = const ซึ่งขัดแย้งกับสมมติฐาน ดังนั้น องค์ประกอบ x เป็นพีชคณิตส่วน D (h) ถ้า h เป็นพีชคณิตส่วน D แล้ว x ก็จะเป็นพีชคณิตส่วน D ด้วยเช่นกัน ซึ่งไม่เป็นเช่นนั้น ดังนั้น h จึงอยู่เหนือ D องค์ประกอบ x เป็นรากของพหุนามดีกรี n ในวงแหวน D (h) (z) พหุนามนี้แยกไม่ออกใน D (h) [z] เพราะไม่เช่นนั้น มันก็จะสลายตัวได้ใน n ในวงแหวน D และเนื่องจากเป็นเส้นตรงในหน่วย h ปัจจัยหนึ่งจึงต้องไม่ขึ้นอยู่กับ h แต่ขึ้นอยู่กับ ซี แต่ไม่มีปัจจัยดังกล่าวเพราะ g (z) และ f (z) เป็นโคไพรม์ ดังนั้น องค์ประกอบ x เป็นพีชคณิตของดีกรี n เหนือสนาม D (h) นี่หมายความว่า (D (x): D (h)) = n สำหรับสิ่งต่อไปนี้ โปรดทราบว่าพหุนาม ไม่มีปัจจัยขึ้นอยู่กับ z เท่านั้น (นั่นคือ อยู่ใน D [z]) ข้อความนี้ยังคงเป็นจริงเมื่อ h ถูกแทนที่ด้วยค่า f (x) / g (x) และคูณด้วยตัวส่วน g (x) จึงเป็นพหุนาม ก. (ซ) ฉ (x) - ฉ (ซ) ก. (x) วงแหวน D ไม่มีปัจจัยขึ้นอยู่กับ z เท่านั้น สามผลสืบเนื่องมาจากทฤษฎีบทที่พิสูจน์แล้ว 1. ระดับของฟังก์ชัน h - f (x) / g (x) ขึ้นอยู่กับฟิลด์ D (h) และ D (x) เท่านั้น และไม่ได้ขึ้นอยู่กับตัวเลือกการสร้างองค์ประกอบ x อย่างใดอย่างหนึ่งหรืออย่างอื่น 2. ความเท่าเทียมกัน D (h) = D (x) จะถือครองก็ต่อเมื่อ h มีดีกรี 1 นั่นคือเป็นฟังก์ชันเศษส่วนเชิงเส้น ซึ่งหมายความว่า: องค์ประกอบกำเนิดของสนาม นอกเหนือจากองค์ประกอบ x แล้ว สามารถเป็นฟังก์ชันเชิงเส้นเศษส่วนใดๆ ของ x และเฉพาะฟังก์ชันดังกล่าวเท่านั้น 3. automorphism ใด ๆ ของสนาม D (x) ปล่อยให้แต่ละองค์ประกอบของสนาม D อยู่ในสถานที่ จะต้องนำองค์ประกอบ x ไปยังองค์ประกอบที่สร้างบางส่วนของสนาม ในทางกลับกัน ถ้า x ถูกแมปกับองค์ประกอบการสร้างบางอย่าง x = (ax + b) / (cx + d) และแต่ละฟังก์ชัน j (x) คือฟังก์ชัน j (x) จะได้รับ automorphism ซึ่งองค์ประกอบทั้งหมดของ D ยังคงอยู่ในสถานที่ เพราะเหตุนี้, automorphisms ทั้งหมดของสนาม D (x) เหนือสนาม D คือการเรียงสับเปลี่ยนเศษส่วนเชิงเส้น x = (ขวาน + b) / (cx + d), โฆษณา - bc ¹ 0 สิ่งสำคัญสำหรับการศึกษาทางเรขาคณิตคือ ทฤษฎีบทของลูรอธ แต่ละช่องกลาง S ซึ่ง DÌSÍD (x) เป็นส่วนขยายเหนือธรรมชาติอย่างง่าย: S = D (q) การพิสูจน์. องค์ประกอบ x ต้องเป็นพีชคณิตมากกว่า S เพราะถ้า h เป็นองค์ประกอบใดๆ ของ S ที่ไม่อยู่ในฟิลด์ D ดังที่แสดงไว้ องค์ประกอบ x เป็นพีชคณิตมากกว่า D (h) และพีชคณิตมากกว่าทั้งหมดบน S ให้ S แยกไม่ออกในวงแหวนพหุนาม [z] พหุนามที่มีสัมประสิทธิ์นำหน้า 1 และรูท x มีรูปแบบ f 0 (z) = z n + a 1 z n -1 + ... + a n (หนึ่ง) ให้เราชี้แจงโครงสร้างของพหุนามนี้ องค์ประกอบ a i เป็นฟังก์ชันตรรกยะของ x โดยการคูณด้วยตัวส่วนร่วม พวกมันสามารถสร้างฟังก์ชันตรรกยะทั้งหมด และนอกจากนี้ ยังสามารถหาพหุนามเทียบกับ x ที่มีเนื้อหา 1 ได้: f (x, z) = b 0 (x) z n + b 1 (x) z n-1 +… + b n (x) ดีกรีของพหุนามนี้เป็น x แทนด้วย m และใน z คูณ n สัมประสิทธิ์ a i = b i / b 0 จาก (1) ไม่สามารถเป็นอิสระจาก x ได้ทั้งหมด มิฉะนั้น x จะเป็นองค์ประกอบเกี่ยวกับพีชคณิตเหนือ D; ดังนั้นหนึ่งในนั้นกล่าวว่า q = a i = b i (x) / b 0 (x), จริง ๆ แล้วควรขึ้นอยู่กับ x; เราเขียนในรูปแบบที่ลดไม่ได้: องศาของพหุนาม g (x) และ h (x) ไม่เกิน m พหุนาม g (z) - qh (z) = g (z) - (g (x) / h (x)) h (z) (ซึ่งไม่ใช่ศูนย์เหมือนกัน) มีราก z = x ดังนั้นจึงหารด้วย f 0 (z) ในวงแหวน S [z] ลงตัว ถ้าเราส่งผ่านจากพหุนามที่เป็นตรรกยะใน x ไปเป็นพหุนามที่เป็นอินทิกรัลใน x ที่มีเนื้อหา 1 แล้ว ความสัมพันธ์ของการหารจะคงอยู่ และเราจะได้ h (x) g (z) -g (x) h (z) = q (x, z) f (x, z) ทางซ้ายมือของความเท่าเทียมกันนี้มีดีกรีเป็น x ไม่เกิน m แต่ทางขวา พหุนาม f มีดีกรี m แล้ว ดังนั้น ระดับของด้านซ้ายมือจึงเท่ากับ m และ q (x, z) ไม่ได้ขึ้นอยู่กับ x อย่างไรก็ตาม ปัจจัยที่ขึ้นอยู่กับ z เท่านั้นไม่สามารถแบ่งด้านซ้ายมือได้ (ดูด้านบน) ดังนั้น q (x, z) จึงเป็นค่าคงที่: h (x) g (z) -g (x) h (z) = qf (x, z) เนื่องจากการมีอยู่ของค่าคงที่ q ไม่สำคัญ โครงสร้างของพหุนาม f (x, z) จึงถูกอธิบายไว้อย่างครบถ้วน ดีกรีของพหุนาม f (x, z) ใน x เท่ากับ m ดังนั้น (ด้วยเหตุผลของความสมมาตร) และดีกรีใน z เท่ากับ m ดังนั้น m = n อย่างน้อยหนึ่งองศาของพหุนาม g (x) และ h (x) จะต้องถึงค่า m จริง ดังนั้นฟังก์ชัน q ต้องมีดีกรี m ใน x ด้วย ดังนั้น ในด้านหนึ่ง เราได้สร้างความเท่าเทียมกัน (D (x): D (q)) = t, และอีกด้านหนึ่ง - ความเท่าเทียมกัน ดังนั้นเนื่องจาก S มี D (q) บทสรุป. ในงานของหลักสูตรมีการพิจารณาการขยายประเภทต่อไปนี้ของฟิลด์หมายเลข P: ส่วนขยายฟิลด์พีชคณิตอย่างง่าย การขยายสนามพีชคณิตแบบผสม ส่วนขยายที่แยกได้และแยกไม่ได้ การขยายสนามที่ไม่มีที่สิ้นสุด การวิเคราะห์งานสามารถสรุปได้บางส่วน ของส่วนขยายที่กล่าวถึงในสองส่วนแรก เช่น: ส่วนขยายพีชคณิตอย่างง่าย ส่วนขยายสุดท้าย ส่วนขยายพีชคณิตแบบผสม ตามมาด้วยส่วนขยายประเภทเหล่านี้ทั้งหมดเกิดขึ้นพร้อมกัน และโดยเฉพาะอย่างยิ่ง ส่วนขยายพีชคณิตอย่างง่ายของฟิลด์ P หมดลงโดยเฉพาะอย่างยิ่ง บรรณานุกรม 1. แอล. คูลิคอฟ. พีชคณิตและทฤษฎีจำนวน.- มอสโก: Vyssh. โรงเรียน พ.ศ. 2522-528-538 2. บี.แอล. ฟาน เดอร์ วาร์เดน. พีชคณิต - ม., 1976 - 138-151s., 158-167s., 244-253s. 3. อี.เอฟ. Shmigirev, S.V. อิกนาโทวิช. ทฤษฎีพหุนาม - Mozyr 2002. สำหรับการเตรียมงานนี้ใช้วัสดุจากไซต์![]() .
.